2024年北师大版数学七年级下册单元清测试(第二章) 培优卷
试卷更新日期:2024-02-01 类型:单元试卷
一、选择题
-
1. 如图,与∠1是同旁内角的是( )
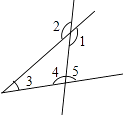 A、∠2 B、∠3 C、∠4 D、∠52. 如图,中, , 顶点 , 分别在直线 , 上.若 , , 则的度数为( )
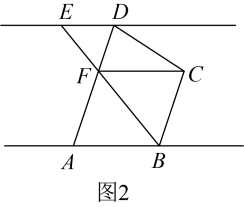
A、∠2 B、∠3 C、∠4 D、∠52. 如图,中, , 顶点 , 分别在直线 , 上.若 , , 则的度数为( ) A、 B、 C、 D、3. 如图,直线 , 菱形和等边在 , 之间,点A,F分别在 , 上,点B,D,E,G在同一直线上:若 , , 则( )
A、 B、 C、 D、3. 如图,直线 , 菱形和等边在 , 之间,点A,F分别在 , 上,点B,D,E,G在同一直线上:若 , , 则( ) A、 B、 C、 D、4. 如图, , 若 , 则的度数为( )
A、 B、 C、 D、4. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、5. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, , 则( )
A、 B、 C、 D、5. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图, , 则( ) A、 B、 C、 D、6. 如图,直线l1//l2 , 直线l3与l1 , l2分别交于A,B两点,过点A作AC⊥l2 , 垂足为C,若∠1=52°,则∠2的度数是( )
A、 B、 C、 D、6. 如图,直线l1//l2 , 直线l3与l1 , l2分别交于A,B两点,过点A作AC⊥l2 , 垂足为C,若∠1=52°,则∠2的度数是( ) A、32° B、38° C、48° D、52°7. 将一对直角三角板如图放置,点C在的延长线上,点B在上, , , , , 则( )
A、32° B、38° C、48° D、52°7. 将一对直角三角板如图放置,点C在的延长线上,点B在上, , , , , 则( ) A、 B、 C、 D、8. 如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为( )
A、 B、 C、 D、8. 如图,AB∥CD∥EF,若∠ABC=130°,∠BCE=55°,则∠CEF的度数为( )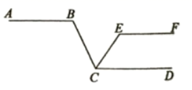 A、95° B、105° C、110° D、115°9. 如图,已知AB∥EF.若∠C=90°,则∠α,∠β,∠γ之间的关系是( )
A、95° B、105° C、110° D、115°9. 如图,已知AB∥EF.若∠C=90°,则∠α,∠β,∠γ之间的关系是( ) A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°10. ①如图1, , 则;②如图2, , 则;③如图3, , 则;④如图4, , 则 . 以上结论正确的个数是( )
A、∠β=∠α+∠γ B、∠α+∠β+∠γ=180° C、∠α+∠β-∠γ=90° D、∠β+∠γ-∠α=90°10. ①如图1, , 则;②如图2, , 则;③如图3, , 则;④如图4, , 则 . 以上结论正确的个数是( ) A、①②③④ B、①②③ C、②③④ D、①②④
A、①②③④ B、①②③ C、②③④ D、①②④二、填空题
-
11. 一副三角板如图摆放,直线 , 则的度数是 .
 12. 如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.
12. 如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.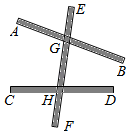 13. 如图,已知AB∥DE∥CF , 若∠ABC=70°,∠CDE=130°,则∠BCD的度数为 .
13. 如图,已知AB∥DE∥CF , 若∠ABC=70°,∠CDE=130°,则∠BCD的度数为 . 14. 两个角α和β的两边互相平行,且一个角α比另一个角β的 多20°,则这个角α的度数为度.15. 如图,将一块直角三角板与一张两边平行的纸条按照如图所示的方式放置,下列结论:;;;其中正确的是 填序号
14. 两个角α和β的两边互相平行,且一个角α比另一个角β的 多20°,则这个角α的度数为度.15. 如图,将一块直角三角板与一张两边平行的纸条按照如图所示的方式放置,下列结论:;;;其中正确的是 填序号 16. 如图,将一张长方形纸片沿折叠后,点、分别落在点、的位置,的延长线与相交于点 , 若 , 则 .
16. 如图,将一张长方形纸片沿折叠后,点、分别落在点、的位置,的延长线与相交于点 , 若 , 则 .
三、解答题
-
17. 如图,点 , 分别在直线 , 上,连接 , , , 分别与 , 相交于点 , , , .
 (1)、求证:;(2)、求证: .18. 如图①.在四边形ABCD中.∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.
(1)、求证:;(2)、求证: .18. 如图①.在四边形ABCD中.∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余. (1)、试判断直线BE与DF的位置关系.并说明理由.(2)、如图②,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为H.试判断∠FBH与∠GBH的大小关系,并说明理由.19. 如图,已知直线AB∥DF,∠D+∠B=180°,
(1)、试判断直线BE与DF的位置关系.并说明理由.(2)、如图②,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为H.试判断∠FBH与∠GBH的大小关系,并说明理由.19. 如图,已知直线AB∥DF,∠D+∠B=180°,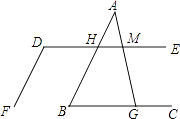 (1)、求证:DE∥BC;(2)、如果∠AMD=75°,求∠AGC的度数.20. 如图,已知BD平分 ,过点A作 交BC于点C,点D为角平分线BD上的一点,连接AD.
(1)、求证:DE∥BC;(2)、如果∠AMD=75°,求∠AGC的度数.20. 如图,已知BD平分 ,过点A作 交BC于点C,点D为角平分线BD上的一点,连接AD.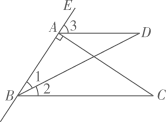 (1)、若 ,求证: .(2)、在(1)的条件下, ,求 的度数.21. 如图,已知点E、F在直线上,点G在线段上,与交于点H , , .
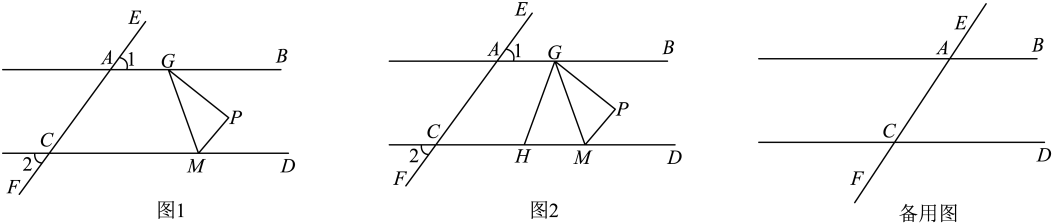
(1)、若 ,求证: .(2)、在(1)的条件下, ,求 的度数.21. 如图,已知点E、F在直线上,点G在线段上,与交于点H , , .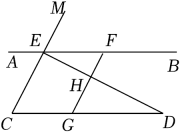 (1)、求证:;(2)、若 , 求的度数.22. 小红同学以“一个含30°的直角三角尺和两条平行线”为背景开展探究活动.如图,在直角三角形ABC中,已知∠BAC=90°,∠ABC=30°,∠ACB=60°,直线 .
(1)、求证:;(2)、若 , 求的度数.22. 小红同学以“一个含30°的直角三角尺和两条平行线”为背景开展探究活动.如图,在直角三角形ABC中,已知∠BAC=90°,∠ABC=30°,∠ACB=60°,直线 . (1)、如图1,直线b与线段AC相交(b不过点C),若∠1=43°,求∠2的度数;(2)、如图2,小红同学把直线b向上平移,使得直线b过点C,若∠1=43°,求∠2的度数;(3)、如图3,小红同学把直线b继续向上平移,使得直线b与线段BC相交(b不过点B),设∠1=x(30°<x<90°),∠2=y,求y与x之间的关系式.
(1)、如图1,直线b与线段AC相交(b不过点C),若∠1=43°,求∠2的度数;(2)、如图2,小红同学把直线b向上平移,使得直线b过点C,若∠1=43°,求∠2的度数;(3)、如图3,小红同学把直线b继续向上平移,使得直线b与线段BC相交(b不过点B),设∠1=x(30°<x<90°),∠2=y,求y与x之间的关系式.