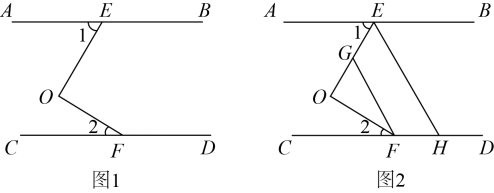2024年北师大版数学七年级下册单元清测试(第二章) 基础卷
试卷更新日期:2024-02-01 类型:单元试卷
一、选择题
-
1. 已知∠α=25°30',则它的补角为( )A、25°30′ B、64° 30' C、164° 30' D、154°30′2. 下面四个图形中,与是对顶角的图形是( )A、
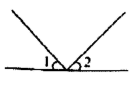 B、
B、 C、
C、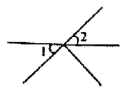 D、
D、 3. 如图所示,在中, , 垂足为点 , , 交于点若 , 则的度数是( )
3. 如图所示,在中, , 垂足为点 , , 交于点若 , 则的度数是( )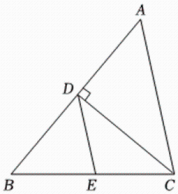 A、 B、 C、 D、4. 如图,将一个含角的直角三角板按如图所示的位置摆放在直尺上.若 , 则的度数为( )
A、 B、 C、 D、4. 如图,将一个含角的直角三角板按如图所示的位置摆放在直尺上.若 , 则的度数为( ) A、 B、 C、 D、5. 如图, , 于点C, , 则的度数为( )
A、 B、 C、 D、5. 如图, , 于点C, , 则的度数为( ) A、 B、 C、 D、6. 如图,直线被射线所截, , 若°,则的度数为( )
A、 B、 C、 D、6. 如图,直线被射线所截, , 若°,则的度数为( ) A、 B、 C、 D、7. 已知 , 点在直线上,点在直线上,于点 , 则的度数是( )
A、 B、 C、 D、7. 已知 , 点在直线上,点在直线上,于点 , 则的度数是( )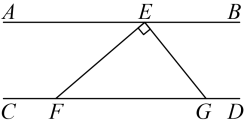 A、 B、 C、 D、8. 如图, , 若 , 则的度数为( )
A、 B、 C、 D、8. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、9. 如图,在正方形网格内,线段的两个端点都在格点上,网格内另有四个格点,下面四个结论中,正确的是( )
A、 B、 C、 D、9. 如图,在正方形网格内,线段的两个端点都在格点上,网格内另有四个格点,下面四个结论中,正确的是( ) A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则10. 如图,直线 , 分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若 , 则的度数是( )
A、连接 , 则 B、连接 , 则 C、连接 , 则 D、连接 , 则10. 如图,直线 , 分别与直线l交于点A,B,把一块含角的三角尺按如图所示的位置摆放,若 , 则的度数是( )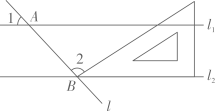 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图所示,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是.
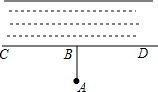 12. 一杆古秤在称物时的状态如图所示,已知 , 则的度数为 .
12. 一杆古秤在称物时的状态如图所示,已知 , 则的度数为 . 13. 如图,若使得 , 则可以添加的一个条件是 .
13. 如图,若使得 , 则可以添加的一个条件是 .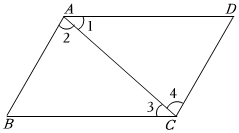 14. 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是.
14. 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是.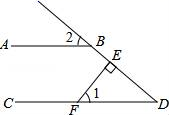 15. 如图,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是.
15. 如图,AB∥CD,CB平分∠ECD,若∠B=26°,则∠1的度数是.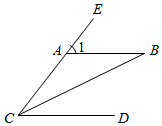 16. 光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面 与水杯下沿 平行,光线变成 ,点G在射线 上, ,则 °.
16. 光线在不同介质中传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面 与水杯下沿 平行,光线变成 ,点G在射线 上, ,则 °.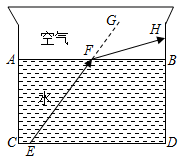
三、解答题
-
17. 如图,在四边形的边的延长线上,连接交于 , 已知 , , 求证:
 18. 如图,已知平分 , 求证:平分 .
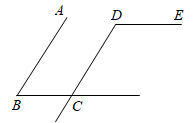
18. 如图,已知平分 , 求证:平分 . 19. 如图, ,点 为直线 , 的交点, .
19. 如图, ,点 为直线 , 的交点, .求证: .
 20. 如图,已知AB∥CD, 若∠C=35∘,AB是∠FAD的平分线.
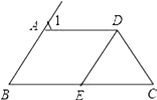
20. 如图,已知AB∥CD, 若∠C=35∘,AB是∠FAD的平分线.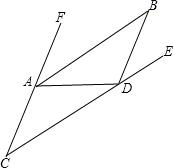 (1)、求∠FAD的度数;(2)、若∠ADB=110∘,求∠BDE的度数.21. 如图,D、E、F分别在△ABC的三条边上,DE∥AB,∠1+∠2=180°.
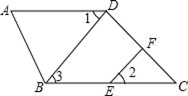
(1)、求∠FAD的度数;(2)、若∠ADB=110∘,求∠BDE的度数.21. 如图,D、E、F分别在△ABC的三条边上,DE∥AB,∠1+∠2=180°.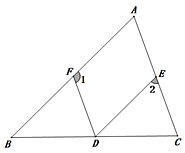 (1)、试说明:DF∥AC;(2)、若∠1=110°,DF平分∠BDE,求∠C的度数.22. 如图1,点是边BC上一点,点D,F是边AC上两点,连接BD,EF,.
(1)、试说明:DF∥AC;(2)、若∠1=110°,DF平分∠BDE,求∠C的度数.22. 如图1,点是边BC上一点,点D,F是边AC上两点,连接BD,EF,. (1)、与平行吗?为什么?(2)、在边取点 , 连接 , 当时(如图2所示),
(1)、与平行吗?为什么?(2)、在边取点 , 连接 , 当时(如图2所示),判断DG与BC的位置关系并说明理由.