2024年北师大版数学七年级下册周测卷(第二章 第3-4节)培优卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 如图, , 于点F , 若 ,则 ( )
 A、 B、 C、 D、2. 如图,直角三角板的直角顶点落在矩形纸片的一边上若 , 则的度数是( )
A、 B、 C、 D、2. 如图,直角三角板的直角顶点落在矩形纸片的一边上若 , 则的度数是( )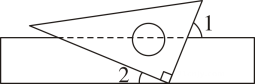 A、 B、 C、 D、3. 把一块直角三角板和一把直尺如图放置,若 , 则的度数等于( )
A、 B、 C、 D、3. 把一块直角三角板和一把直尺如图放置,若 , 则的度数等于( ) A、 B、 C、 D、4. 如图,是的平分线, , , 则的度数是( )
A、 B、 C、 D、4. 如图,是的平分线, , , 则的度数是( ) A、50° B、40° C、35° D、45°5. 如图,直线直线n,点A在直线n上,点B在直线m上,连接 , 过点A作 , 交直线m于点C.若 , 则的度数为( )
A、50° B、40° C、35° D、45°5. 如图,直线直线n,点A在直线n上,点B在直线m上,连接 , 过点A作 , 交直线m于点C.若 , 则的度数为( )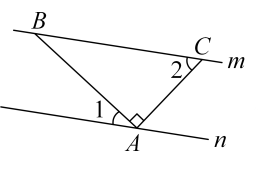 A、 B、 C、 D、6. 如图,是直尺的两边, , 把三角板的直角顶点放在直尺的边上,若 , 则的度数是( )
A、 B、 C、 D、6. 如图,是直尺的两边, , 把三角板的直角顶点放在直尺的边上,若 , 则的度数是( ) A、 B、 C、 D、7. 将一副三角板按下图所示摆放在一组平行线内, , , 则的度数为( )
A、 B、 C、 D、7. 将一副三角板按下图所示摆放在一组平行线内, , , 则的度数为( )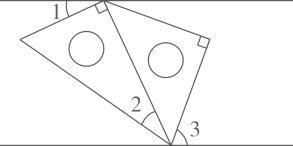 A、55° B、65° C、70° D、75°8. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ).
A、55° B、65° C、70° D、75°8. 如图,小颖按如下方式操作直尺和含角的三角尺,依次画出了直线a,b,c.如果 , 则的度数为( ). A、 B、 C、 D、9. 如图, , 若 , 则的度数为( )
A、 B、 C、 D、9. 如图, , 若 , 则的度数为( ) A、 B、 C、 D、10. 如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )
A、 B、 C、 D、10. 如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )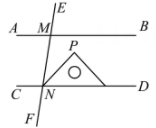 A、15° B、25° C、35° D、45°
A、15° B、25° C、35° D、45°二、填空题
-
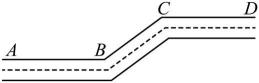
11. 如图,一条公路经两次转弯后,方向未变.第一次的拐角是 , 第二次的拐角是°.
 12. 将一副三角尺如图所示放置,其中 , 则度.
12. 将一副三角尺如图所示放置,其中 , 则度.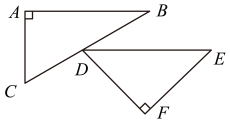 13. 某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线 , 等反射后都沿着与平行的方向射出.若 , , 则 .
13. 某些灯具的设计原理与抛物线有关.如图,从点照射到抛物线上的光线 , 等反射后都沿着与平行的方向射出.若 , , 则 . 14. 如图, , 则度.
14. 如图, , 则度. 15. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 .
15. 1.如图,直线a∥b,点C、A分别在直线a、b上,AC⊥BC,若∠1=50°,则∠2的度数为 . 16. 如图,若AB∥CD,∠A=110°,则∠1=°.
16. 如图,若AB∥CD,∠A=110°,则∠1=°.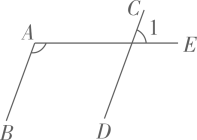
三、解答题
-
17. 如图,已知直线 , .
 (1)、与平行吗?请说明理由;(2)、若 , 求的度数.18. 已知直线 , 和 , 分别交于 , 点,点 , 分别在线 , 上,且位于的左侧,点在直线上,且不和点 , 重合.
(1)、与平行吗?请说明理由;(2)、若 , 求的度数.18. 已知直线 , 和 , 分别交于 , 点,点 , 分别在线 , 上,且位于的左侧,点在直线上,且不和点 , 重合. (1)、如图 , 点在线段上, , , 求的度数.(2)、如图 , 当点在直线上运动时,试判断 , , 的数量关系,直接写出结果,不需要说明理由.19. 如图,已知∠A=∠C,AD⊥BE,BC⊥BE,点E,D,C在同一条直线上.
(1)、如图 , 点在线段上, , , 求的度数.(2)、如图 , 当点在直线上运动时,试判断 , , 的数量关系,直接写出结果,不需要说明理由.19. 如图,已知∠A=∠C,AD⊥BE,BC⊥BE,点E,D,C在同一条直线上.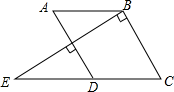 (1)、判断AB与CD的位置关系,并说明理由.(2)、若∠ABC=120°,求∠BEC的度数.20. 如图, , .
(1)、判断AB与CD的位置关系,并说明理由.(2)、若∠ABC=120°,求∠BEC的度数.20. 如图, , . (1)、试判断与的位置关系,并说明理由;(2)、若 , , 求的度数.21. 如图,已知 , 于点 , .
(1)、试判断与的位置关系,并说明理由;(2)、若 , , 求的度数.21. 如图,已知 , 于点 , . (1)、求证:;(2)、连接 , 若 , 且 , 求的度数.22. 已知:点C是∠AOB的OA边上一点(点C不与点O重合),点D是∠AOB内部一点,射线CD不与OB相交.
(1)、求证:;(2)、连接 , 若 , 且 , 求的度数.22. 已知:点C是∠AOB的OA边上一点(点C不与点O重合),点D是∠AOB内部一点,射线CD不与OB相交.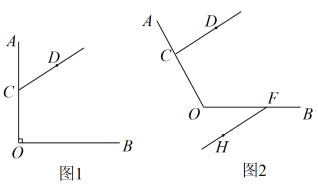 (1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).
(1)、如图1,∠AOB=90°,∠OCD=120°,过点O作射线OE,使得OE//CD.(其中点E在∠AOB内部).①依据题意,补全图1;
②直接写出∠BOE的度数.
(2)、如图2,点F是射线OB上一点,且点F不与点O重合,当时,过点F作射线FH,使得FH//CD(其中点H在∠AOB的外部),用含的代数式表示∠OCD与∠BFH的数量关系,并证明.23. 已知一个角的两边与另一个角的两边分别平行,请结合图形回答下列问题: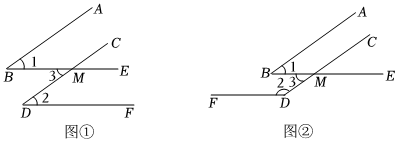 (1)、如图 , , , 直接写出与的关系 ;(2)、如图 , , , 猜想与的关系,并说明理由;(3)、由(1)(2),我们可以得出结论:一个角的两边与另一个角的分别平行,那么这两个角 ;(4)、应用:两个角的两边分别平行,且一个角比另一个角的倍少 , 求出这两个角的度数分别是多少度?
(1)、如图 , , , 直接写出与的关系 ;(2)、如图 , , , 猜想与的关系,并说明理由;(3)、由(1)(2),我们可以得出结论:一个角的两边与另一个角的分别平行,那么这两个角 ;(4)、应用:两个角的两边分别平行,且一个角比另一个角的倍少 , 求出这两个角的度数分别是多少度?