2024年北师大版数学七年级下册周测卷(第二章 第3-4节)基础卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 如图,已知AB∥CD,则图中与∠1相等的角有( )
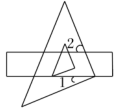
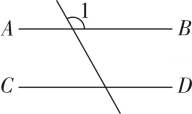 A、5个 B、4个 C、3个 D、2个2. 已知直线 m∥n.将一把含30°角的三角尺ABC按如图所示的方式放置(∠ABC=30°),其中A、B两点分别落在直线m、n上.若∠1=20°,则∠2的度数为( )
A、5个 B、4个 C、3个 D、2个2. 已知直线 m∥n.将一把含30°角的三角尺ABC按如图所示的方式放置(∠ABC=30°),其中A、B两点分别落在直线m、n上.若∠1=20°,则∠2的度数为( ) A、10° B、20° C、30° D、40°3. 如图,已知∠1=70°,CD∥BE,则∠B的度数为( )
A、10° B、20° C、30° D、40°3. 如图,已知∠1=70°,CD∥BE,则∠B的度数为( )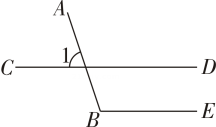 A、70° B、100° C、110° D、120°4. 如果两条直线被第三条直线所截,那么( )A、同位角相等 B、内错角相等 C、同旁内角互补 D、对顶角相等5. 将一直角三角板与两边平行的纸条如图所示放置,若∠1=55°,则∠2的度数为( )
A、70° B、100° C、110° D、120°4. 如果两条直线被第三条直线所截,那么( )A、同位角相等 B、内错角相等 C、同旁内角互补 D、对顶角相等5. 将一直角三角板与两边平行的纸条如图所示放置,若∠1=55°,则∠2的度数为( )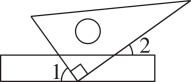 A、135° B、130° C、45° D、35°6. 下列图形中,由 , 能得到的是( )A、
A、135° B、130° C、45° D、35°6. 下列图形中,由 , 能得到的是( )A、 B、
B、 C、
C、 D、
D、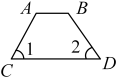 7. 如图,已知 , , 则等于( )
7. 如图,已知 , , 则等于( ) A、 B、 C、 D、8. 如图,已知 , , , 则的度数是( )
A、 B、 C、 D、8. 如图,已知 , , , 则的度数是( )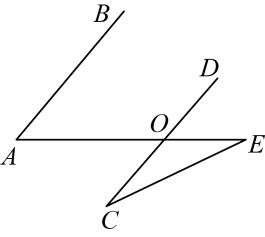 A、 B、 C、 D、9. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、
A、 B、 C、 D、9. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、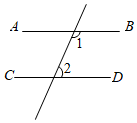 B、
B、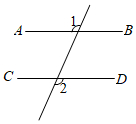 C、
C、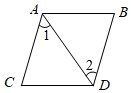 D、
D、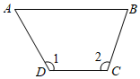 10. 墨墨想在纸上作∠A1O1B1等于已知的∠AOB,步骤有:①画射线O1M.②以点O为圆心,以任意长为半径画弧,交OA于点C1 , 交OB于点D;③以点A1为圆心,以CD为半径画弧,与已画的弧交于点B1 , 作射线O1B1;④以点O1为圆心,以OC为半径画弧,交O1M于点A1 , 在上述的步骤中,作∠A1O1B1的正确顺序应为( )A、①④②③ B、②③④① C、②①④③ D、①③④②
10. 墨墨想在纸上作∠A1O1B1等于已知的∠AOB,步骤有:①画射线O1M.②以点O为圆心,以任意长为半径画弧,交OA于点C1 , 交OB于点D;③以点A1为圆心,以CD为半径画弧,与已画的弧交于点B1 , 作射线O1B1;④以点O1为圆心,以OC为半径画弧,交O1M于点A1 , 在上述的步骤中,作∠A1O1B1的正确顺序应为( )A、①④②③ B、②③④① C、②①④③ D、①③④②二、填空题
-
11. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若 , 则的度数是 .
 12. 一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=度.
12. 一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=150°,则∠ABC=度.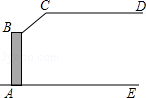 13. 将一副三角尺和直尺按如图所示摆放,则°.
13. 将一副三角尺和直尺按如图所示摆放,则°. 14. 如图, , , , 垂足为点 , 则的大小为 .
14. 如图, , , , 垂足为点 , 则的大小为 . 15. 如图, , , , , 则.
15. 如图, , , , , 则. 16. 如图是我们常用的折叠式小刀,刀柄外形左侧是一个长方形的一角,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成与若 , 则 .
16. 如图是我们常用的折叠式小刀,刀柄外形左侧是一个长方形的一角,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成与若 , 则 .
三、解答题
-
17. 如图,已知 , . 求证: .
 18. 如图所示,与互补,.求证:.
18. 如图所示,与互补,.求证:. 19. 如图,在中,D是边上一点,G是边上一点,过点G作交于点F,E是边上一点,连接 , .
19. 如图,在中,D是边上一点,G是边上一点,过点G作交于点F,E是边上一点,连接 , . (1)、判断与是否平行,并说明理由.(2)、若平分 , , , 求的度数.20. 如图,直线分别交直线于点E,点F, , 平分交于点G.
(1)、判断与是否平行,并说明理由.(2)、若平分 , , , 求的度数.20. 如图,直线分别交直线于点E,点F, , 平分交于点G.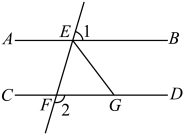 (1)、求证: .(2)、若 , 求的度数.21. 如图, , , .
(1)、求证: .(2)、若 , 求的度数.21. 如图, , , . (1)、求的度数;(2)、若平分 , 求的度数.22. 如图,AB∥DG,∠1+∠2=180°,
(1)、求的度数;(2)、若平分 , 求的度数.22. 如图,AB∥DG,∠1+∠2=180°,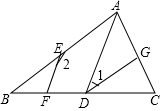 (1)、求证:AD∥EF;(2)、若DG是∠ADC的平分线,∠2=150°,求∠B的度数.23. 如图, AC平分∠MAE,交DB于点F.
(1)、求证:AD∥EF;(2)、若DG是∠ADC的平分线,∠2=150°,求∠B的度数.23. 如图, AC平分∠MAE,交DB于点F. (1)、若AB∥CE,∠BAE=50°,求∠ACE的度数;(2)、若∠AFB=∠CAM,说明∠ACE=∠BDE的理由.24. 已知:如图,直线与分别相交于点E,F.
(1)、若AB∥CE,∠BAE=50°,求∠ACE的度数;(2)、若∠AFB=∠CAM,说明∠ACE=∠BDE的理由.24. 已知:如图,直线与分别相交于点E,F. (1)、如图1,若 , , 和的位置关系为;(2)、在(1)的情兄下,若点P是平面内的一个动点,连接 , 探索三个角之间的关系;
(1)、如图1,若 , , 和的位置关系为;(2)、在(1)的情兄下,若点P是平面内的一个动点,连接 , 探索三个角之间的关系;①当点P在图2的位置时,可得;
请阅读下面的解答过程,并填空(理由或数学式):
解:如图2、过点P作 ,
则( ).
∵(已知),(作图),
∴( ).
∴ .
∴( ).
即;
②当点P在图3的位置时,求三个角之间有何数量关系;
③当点P在图4的位置时,请三个角之间的关系.