2024年北师大版数学七年级下册周测卷（第二章 第1-2节）基础卷
试卷更新日期：2024-02-01 类型：同步测试
一、选择题
-
1. 下列图形中，能够相交的是（ ）A、
B、
C、
D、
2. 下面四个图形中，∠1与∠2是对顶角的是（ ）A、
B、
C、
D、
3. 如图，直线 ， 相交于点O ， ， 则的度数是（ ）
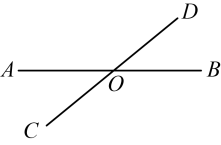A、 B、 C、 D、4. 若∠A＝23°，则∠A余角的大小是（ ）A、57° B、67° C、77° D、157°5. 下列生活中的实例，数学原理解释错误的一项是（ ）A、从一条河向一个村庄引一条最短的水渠．可用的数学原理是：在同一平面内，过一点有且只有一条直线垂直于已知直线 B、两个村庄之间修一条最短的公路．可用的数学原理是：两点之间线段最短 C、把一根木条固定到墙上需要两颗钉子．可用的数学原理是：两点确定一条直线 D、从一个物流仓库向高速公路修一条最短的马路．可用的数学原理是：连结直线外一点与直线上各点的所有线段中，垂线段最短6. 如图，已知∠1=50°，下列条件中，能使AB∥CD的是（ ）
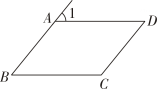A、∠BAD=130° B、∠B=50° C、∠C=130° D、∠D=50°7. 如图所示的四个图形中，∠1和∠2是同位角的为（ ）
A、②③ B、①②③ C、①②④ D、①④8. 如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是（ ）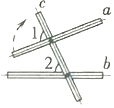
A、10° B、20° C、50° D、70°9. 在同一平面内，过直线外一点作的垂线 ， 再过作的垂线 ， 则直线与的位置关系是（ ）A、相交 B、相交且垂直 C、平行 D、不能确定10. 如图所示，下列推理中，正确的是（ ）
A、∵∠A+∠D=180°，∴AD∥BC B、∵∠C+∠D=180°，∴AB∥CD C、∵∠A+∠D=180°，∴AB∥CD D、∵∠A+∠C=180°，∴AB∥CD二、填空题
-
11. 若一个角的余角是 ， 则这个角的补角为 ．12. 在跳远比赛中，某运动员的起跳点为A，落地点为B，如图，量出落地点B到起跳点A所在直线l的距离BH，即为该运动员的成绩．此时，BHBA(填“>”或“<”)，理由：.
13. 如图，已知直线AB，CD相交于点O，OE是射线，若∠1=30°，∠2=60°，则OE与AB 的位置关系是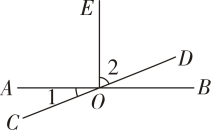
14. 一节数学实践课上，老师让同学们用两个大小、形状都相同的三角板画平行线AB、CD，并要说出自己做法的依据，小奇、小妙两位同学的做法如图：小奇说：“我做法的依据是：内错角相等，两直线平行．”小妙做法的依据是
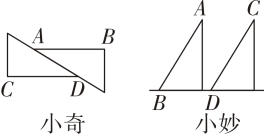15. 如图，已知 ， 请你添加一个条件： ， 使得 ．
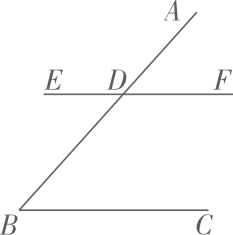16. 如图，在三角形中，点 ， ， 分别在 ， ， 上，连接 ， ， ， 则下列条件；；；；；不能判定的有填序号 ．
三、解答题
-
17. 如图：O为直线AB上一点， ，OC是 的平分线.求： 的度数
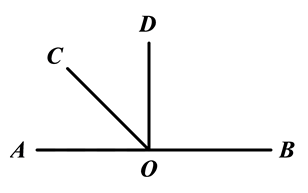18. 如图：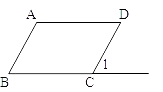
(1)、如果∠1=∠D，那么∥；
(2)、如果∠1=∠B，那么∥；
(3)、如果∠A+∠B=180º，那么∥；
(4)、如果∠A+∠D=180º，那么∥；
19. 如图，∠DAE＝∠E，∠B＝∠D，试说明AB∥DC．
请完善解答过程，并在括号内填写相应的理论依据．
解：∵∠DAE＝∠E，（已知）
∴ ▲ ∥BE．（ ）
∴∠D＝ ▲ ． （ ）
∵∠B＝∠D，（已知）
∴∠B＝ ▲ ． （等量代换）
∴AB∥DC．（ ）
20. 如图，CE⊥DG，垂足为G，∠BAF=50°，∠ACE=140°．CD与AB平行吗？为什么？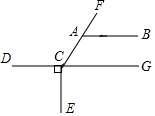
21. 如图，已知BC平分∠ACD，且∠1=∠2，则AB∥CD，请说明理由．
