2024年北师大版数学七年级下册周测卷(第一章 第5-7节)培优卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 下列多项式相乘,能用平方差公式计算的是( )A、 B、 C、 D、2. 若k为任意整数,则的值总能( )A、被2整除 B、被3整除 C、被5整除 D、被7整除3. 观察下面图形,从图1到图2可用式子表示为( )
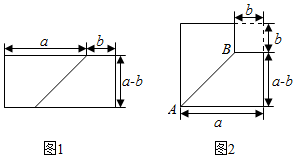 A、(a+b)(a﹣b)=a2﹣b2 B、a2﹣b2=(a+b)(a﹣b) C、(a+b)2=a2+2ab+b2 D、a2+2ab+b2=(a+b)24. 如图,大正方形的边长为m,小正方形的边长为n,x,y表示四个相同长方形的两边长(x>y) .则①x-y=n;②xy= ;③x2-y2=mn;④x2+y2= , 中正确的是( )
A、(a+b)(a﹣b)=a2﹣b2 B、a2﹣b2=(a+b)(a﹣b) C、(a+b)2=a2+2ab+b2 D、a2+2ab+b2=(a+b)24. 如图,大正方形的边长为m,小正方形的边长为n,x,y表示四个相同长方形的两边长(x>y) .则①x-y=n;②xy= ;③x2-y2=mn;④x2+y2= , 中正确的是( ) A、①②③ B、①②④ C、①③ D、①②③④5. 已知(a+b)2=49,a2+b2=25,则ab=( )A、24 B、48 C、12 D、26. 将多项式4x2+1再加上一项,使它能分解因式成(a+b)2的形式,以下是四位学生所加的项,其中错误的是( )A、2x B、﹣4x C、4x4 D、4x7. 若 , , 在下列判断结果正确的是( )A、 B、 C、 D、无法判断8. 如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个长方形(不重叠、无缝隙),则该长方形的面积是( )
A、①②③ B、①②④ C、①③ D、①②③④5. 已知(a+b)2=49,a2+b2=25,则ab=( )A、24 B、48 C、12 D、26. 将多项式4x2+1再加上一项,使它能分解因式成(a+b)2的形式,以下是四位学生所加的项,其中错误的是( )A、2x B、﹣4x C、4x4 D、4x7. 若 , , 在下列判断结果正确的是( )A、 B、 C、 D、无法判断8. 如图,从边长为(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a>1),剩余部分沿虚线又剪拼成一个长方形(不重叠、无缝隙),则该长方形的面积是( ) A、2cm2 B、2a(cm2) C、4a(cm2) D、(a2-1)cm29. 4张长为a、宽为 的长方形纸片,按如图的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则a、b满足( )
A、2cm2 B、2a(cm2) C、4a(cm2) D、(a2-1)cm29. 4张长为a、宽为 的长方形纸片,按如图的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则a、b满足( )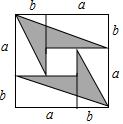 A、 B、 C、 D、10. 若 ,则 ( )A、12 B、10 C、8 D、6
A、 B、 C、 D、10. 若 ,则 ( )A、12 B、10 C、8 D、6二、填空题
-
11. 已知 ,则 .12. 1261年,我国宋朝数学家杨辉在其著作《详解九章算法》中提到了如图所示的数表,人们将这个数表称为“杨辉三角”.

观察“杨辉三角”与右侧的等式图,根据图中各式的规律,展开的多项式中各项系数之和为 .
13. 一个长方形,它的面积为6a2﹣9ab+3a,已知这个长方形的长为3a,则宽为 .14. 已知a+ =3,则a2+ 的值是 .15. 如图①,在边长为a的正方形中剪去一个边长为b的小正方形,然后把剩下部分沿图中虚线剪开后拼成如图②所示的梯形、通过计算图①、图②中阴影部分的面积,可以得到的代数恒等式为 .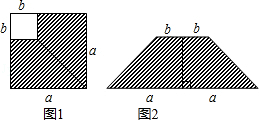 16. 若实数m满足(m-2023)2+(2024-m)2=2025,则(m-2023)(2024-m)= .
16. 若实数m满足(m-2023)2+(2024-m)2=2025,则(m-2023)(2024-m)= .三、解答题
-
17. 用乘法公式计算:(1)、40 ×39 ;(2)、 .18. 先化简,再求值: , 其中 ,19. 先化简,再求值: , 其中x=1,y=-220. 先化简,再求值: , 其中 , .21. 先化简,再求值:
,其中 ,
22. 观察以下等式:第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
……
按照以上规律,解决下列问题:
(1)、写出第5个等式: .(2)、写出你猜想的第个等式(用含的式子表示),并证明.23. 聪聪和同学们用2张型卡片、2张型卡片和1张型卡片拼成了如图所示的长方形.其中型卡片是边长为的正方形;型卡片是长方形;型卡片是边长为的正方形. (1)、请用含a、b的代数式分别表示出型卡片的长和宽;(2)、如果 , , 请求出他们用5张卡片拼出的这个长方形的面积.24. 如图,将两个长方形用不同方式拼成图和图两个图形.
(1)、请用含a、b的代数式分别表示出型卡片的长和宽;(2)、如果 , , 请求出他们用5张卡片拼出的这个长方形的面积.24. 如图,将两个长方形用不同方式拼成图和图两个图形. (1)、若图中的阴影部分面积为 , 则图中的阴影部分面积为 用含字母 , 的代数式表示;(2)、由你可以得到的等式是 ;(3)、根据你所得到的等式解决下面的问题:
(1)、若图中的阴影部分面积为 , 则图中的阴影部分面积为 用含字母 , 的代数式表示;(2)、由你可以得到的等式是 ;(3)、根据你所得到的等式解决下面的问题:若 , , 则 _▲_ ;
计算: .
解方程: .25. 图1,是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形. (1)、图2中阴影部分的面积为.(2)、观察图2,三个代数式(m+n)2 , (m-n)2 , mn之间的等量关系是.(3)、若x+y=-6,xy=2.75,求x-y的值.(4)、观察图3,你能得到怎样的代数恒等式呢?
(1)、图2中阴影部分的面积为.(2)、观察图2,三个代数式(m+n)2 , (m-n)2 , mn之间的等量关系是.(3)、若x+y=-6,xy=2.75,求x-y的值.(4)、观察图3,你能得到怎样的代数恒等式呢?