2024年北师大版数学七年级下册周测卷（第一章第3-4节）培优卷

试卷更新日期：2024-02-01 类型：同步测试

进入出卷网下载

一、选择题

1. 下列运算中，结果正确的是（）

A、 $2 m^{2} + m^{2} = 3 m^{4}$ B、 $m^{2} · m^{4} = m^{3}$ C、 $m^{4} \div m^{2} = m^{2}$ D、 $(m^{2})^{4} = m^{6}$

查看试题解析
2. 若 $a \neq 0$ ，下列计算正确的是（）

A、 $(- a)^{0} = 1$ B、 $a^{6} \div a^{3} = a^{2}$ C、 $a^{- 1} = - a$ D、 $a^{6} - a^{3} = a^{3}$

查看试题解析
3. 光年是天文学上的一种距离单位，一光年是指光在一年内走过的路程，约等于 $9.46 \times 1 0^{12} k m$ ．下列正确的是（）

A、 $9.46 \times 1 0^{12} - 10 = 9.46 \times 1 0^{11}$ B、 $9.46 \times 1 0^{12} - 0.46 = 9 \times 1 0^{12}$ C、 $9.46 \times 1 0^{12}$ 是一个12位数 D、 $9.46 \times 1 0^{12}$ 是一个13位数

查看试题解析
4. 计算 $| - 5 | + 2^{0}$ 的结果是（）

A、-3 B、7 C、-4 D、6

查看试题解析
5. 设有边长分别为a和b( $a > b$ )的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张．如图所示要拼一个边长为 $a + b$ 的正方形，需要1张A类纸片、1张B类纸片和2张C类纸片．若要拼一个长为 $3 a + b$ 、宽为 $2 a + 2 b$ 的矩形，则需要C类纸片的张数为（）

A、6 B、7 C、8 D、9

查看试题解析
6. 使 $(x^{2} + p x + 8) (x^{2} - 3 x + q)$ 乘积中不含 $x^{2}$ 与 $x^{3}$ 项的p，q的值是（）

A、 $p = 0$ ， $q = 0$ B、 $p = 3$ ， $q = 1$ C、 $p = - 3$ ， $q = - 9$ D、 $p = - 3$ ， $q = 1$

查看试题解析
7. 如果长方形的长为(4a²-2a+1)，宽为(2a+1)，则这个长方形的面积为（）

A、8a³-4a²+2a-1 B、8a³+4a²-2a-1 C、8a³-1 D、8a³+1

查看试题解析
8. 如图，美美不小心在课后作业的第1题滴了一点墨水，留下一道残缺不全的题目，则被墨水覆盖的部分为（）

A、 $x^{3} - x^{2} + x$ B、 $- x^{3} - x^{2} + x$ C、 $- x^{3} + x^{2} - x$ D、 $x^{3} + x^{2} - x$

查看试题解析
9. 已知 $x^{m} = a$ ， $x^{n} = b (x \neq 0)$ ，则 $x^{3 m - 2 n}$ 的值等于（）

A、 $3 a - 2 b$ B、 $a^{3} - b^{2}$ C、 $a^{3} b^{2}$ D、 $\frac{a^{3}}{b^{2}}$

查看试题解析
10. 将3^-1 ， (-4)⁰ ， (-2)² ，这三个数按从小到大的顺序排列，正确的结果是（）

A、3^-1<(-4)⁰<(-2)² B、(-4)⁰< 3^-1<(-2)² C、(-4)⁰<(-2)²<3^-1 D、(-2)²<3^-1<(-4)⁰

查看试题解析

二、填空题

11. 已知a^m=3，aⁿ=2，则a^2m^﹣ⁿ的值为．

查看试题解析
12. 若3a-2b+4c=3，则27^a÷9^b×81^c的值为.

查看试题解析
13. 已知m+n= $\frac{1}{2}$ mn，则(m-2)(n-2)= ．

查看试题解析
14. 如果 $m + n = 2 \frac{1}{3}$ ， $m - n = 3 \frac{1}{2}$ ，则 $2 - \frac{3}{7} m - \frac{3}{7} n$ =.

查看试题解析
15. 阅读以下问题的解答过程：若多项式 $2 x^{2} - x + a$ 能被 $x - 2$ 整除，求常数a的值．解法如下：
∵二次三项式 $2 x^{2} - x + a$ 中最高次项是 $2 x^{2}$ ，已知因式 $(x - 2)$ 中最高次项是x ，

又∵ $x \cdot 2 x = 2 x^{2}$ ，

∴另一因式的最高次项应为 $2 x$ ．因此，可设另一因式为 $(2 x + m)$ （其中m是常数项）．

即得， $2 x^{2} - x + a = (x - 2) (2 x + m)$ ． ∴ $2 x^{2} - x + a = 2 x^{2} + (m - 4) x - 2 m$ ．

可得 $- 1 = m - 4$ ， $a = - 2 m$ ． ∴ $m = 3$ ， $a = - 6$ ．

仿照以上解题方法，解答以下问题：已知 $3 x^{3} + k x^{2} + 1$ 被 $3 x - 1$ 整除，则k的值为．

查看试题解析
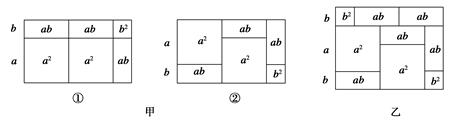
16. 下图中的四边形均为长方形，根据图形的面积关系，写出一个正确的等式：．

查看试题解析

三、解答题

17. 计算： $- 2^{2} + {(π - 2023)}^{0} - {(- \frac{1}{2})}^{- 1}$ ．

查看试题解析
18. 计算： ${(\frac{1}{2})}^{- 1} + {(- 1)}^{2023} + {(π - 3.14)}^{0}$ ；

查看试题解析
19. 计算： $- 3^{2} - {(\frac{1}{2})}^{- 2} + {(2023 - π)}^{0} - | - 2 |$ ．

查看试题解析
20. 计算： $| - 1 | + {(3.14 - π)}^{0} + {(\frac{1}{3})}^{- 2} + {(- 1)}^{2023}$ ．

查看试题解析
21. 先化简，再求值：
(2a-3b)(3a+2b)-(2a+b)(a-2b)，其中a=-2，b=-1．

查看试题解析
22. 先化简，再求值：
$- 4 x (x^{2} - 2 x - 1) + x (2 x + 5) (2 x - 5)$ ，其中 $x = - 1$ ．

查看试题解析
23. 阅读下列文字，并解决问题。
已知x²y=3，求2xy（x⁵y²-3x³y-4x）的值.
分析：考虑到满足x²y=3的x，y的可能值较多，不可以逐一代入求解，故考虑整体思想，将x²y=3整体代入.
解：2xy（x⁵y²-3x³y-4x）
=2x⁶y³-6x⁴y²-8x²y
=2（x²y）³-6（x²y）²-8x²y，
将x²y=3代入
原式=2×3³-6×3²-8×3=-24.
请你用上述方法解决下面问题：
已知ab=3，求（2a³b²-3a²b+4a）·（-2b）的值.

查看试题解析
24. 如图

(1)、数学课堂上老师留了一道数学题，如图①，用式子表示空白部分的面积，
甲、乙两名同学表示的式子是：甲：10×6-10x-6x；乙：（10- x）（6-x）．
正确的学生是

(2)、如图②，有一块长为（8a+3b）米。宽为（7a-3b）米的长方形空地，计划修筑东西、南北走向的两条道路。其余进行绿化。已知两条道路的宽分别为2a米和3a米，求绿化的面积．（用含a，b的式子来表示）

查看试题解析
25. 我们规定： $a^{- p} = \frac{1}{a^{p}} (a \neq 0)$ ，即 $a$ 的负 $p$ 次幂等于 $a$ 的 $p$ 次幂的倒数．例： $4^{- 2} = \frac{1}{4^{2}}$ ．

(1)、计算： ${(- 2)}^{- 2} =$ ；若 $2^{- p} = \frac{1}{8}$ ，则 $p =$ ；

(2)、若 $a^{- 2} = \frac{1}{16}$ ，求 $a$ 的值；

(3)、若 $a^{- p} = \frac{1}{9}$ ，且 $a$ ， $p$ 为整数，求满足条件的 $a$ ， $p$ 的值．

查看试题解析
26. 阅读材料并解答下列问题.
你知道吗？一些代数恒等式可以用平面图形的面积来表示，例如（2a＋b）（a＋b）＝2a²＋3ab＋b²就可以用图甲中的①或②的面积表示.

(1)、请写出图乙所表示的代数恒等式；

(2)、画出一个几何图形，使它的面积能表示（a＋b）（a＋3b）＝a²＋4ab＋3b²；

(3)、请仿照上述式子另写一个含有a，b的代数恒等式，并画出与之对应的几何图形.

查看试题解析

2024年北师大版数学七年级下册周测卷（第一章 第3-4节）培优卷

一、选择题

二、填空题

三、解答题

2024年北师大版数学七年级下册周测卷（第一章第3-4节）培优卷