2024年北师大版数学七年级下册周测卷(第一章 第1-2节)培优卷
试卷更新日期:2024-02-01 类型:同步测试
一、选择题
-
1. 计算a3•a的结果是( )A、a2 B、a3 C、a4 D、a52. 不一定相等的一组是( )A、 与 B、 与 C、 与 D、 与3. 若2n+2n+2n+2n=2,则n=( )A、﹣1 B、﹣2 C、0 D、4. 计算:( )A、 B、 C、 D、5. 下列运算中,结果正确的是( )A、 B、 C、 D、6. 已知 ,则 ( )A、1 B、6 C、7 D、127. 已知a=833 , b=1625 , c=3219 , 则有( )A、a<b<c B、c<b<a C、c<a<b D、a<c<b8. 1993+9319的个位数字是( )
A、2 B、4 C、6 D、89. 如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出个球放入乙袋,再从乙袋中取出个球放入丙袋,最后从丙袋中取出个球放入甲袋,此时三只袋中球的个数相同,则的值等于( )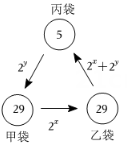 A、128 B、64 C、32 D、1610. 为了求 的值,可设 ,等式两边同乘以 ,得 ,所以得 ,所以 ,即: = .仿照以上方法求 的值为( )A、 B、 C、 D、
A、128 B、64 C、32 D、1610. 为了求 的值,可设 ,等式两边同乘以 ,得 ,所以得 ,所以 ,即: = .仿照以上方法求 的值为( )A、 B、 C、 D、二、填空题
-
11. 若 , , 则 .12. 若am= 4,a2m+n= 128,则an=13. 计算: .14. 观察下列等式:2+22=23-2,2+22+23=24-2,2+22+23+24=25-2…,若250=m , 则2101+2101+2102+…+2201= . (用含m的代数式表示)15. 已知 , 则 .16. 若x,y均为实数, , 则.
三、解答题
-
17. 若与与的积与是同类项,求、的值.18. 已知2a=5,2b=1,求2a+b+3的值.19. 已知 , 求x的值;20. 已知n为正整数,且x2n=2,求(3x3n)2-4(x2)2n的值。21. 已知 , , , 比较a,b,c的大小.22. 已知n为正整数,且x2n=4(1)、求xn-3·x3(n+1)的值;(2)、求9(x3n)2-13(x2)2n的值.23.
记M(1)=-2,M(2)=(-2)×(-2),M(3)=(-2)×(-2)×(-2),……
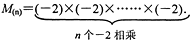
(Ⅰ) 计算:M(5)+M(6);
(Ⅱ) 求2M(2015)+M(2016)的值:
(Ⅲ) 说明2M(n)与M(n+1)互为相反数.
24. 阅读材料:我们已经学过幂的相关运算,其中幂的乘方是重要的性质之一,用式子表示为:(m、n为正整数),由此,幂的乘方运算反过来也是成立的,用式子表示为:(m、n为正整数),逆用幂的乘方的方法是:幂的底数不变,将幂的指数分解成两个因数的乘积,再转化成幂的乘方的形式.如 , 至于选择哪一个变形结果,要具体问题具体分析.例如,判断的末尾数字,我们可以采用如下的方法:解析:的末尾数字等于的末尾数字
∵ , 又(n为正整数)的末尾数字均为6,
∴的末尾数字是的末尾数字,即为8.
∴的末尾数字为8
根据以上阅读材料,回答下列问题:
(1)、逆用幂的乘方,写出的末尾数字(2)、试判断的末尾数字25. 我们知道,一般的数学公式、法则、定义可以正向运用,也可以逆向运用.对于“同底数幂的乘法”“幂的乘方”“积的乘方”这几个法则的逆向运用表现为 , , (m , n为正整数).请运用这个思路和幂的运算法则解决下列问题:
(1)、已知 , 请把用“<”连接起来: .(2)、若 , 求的值.(3)、计算: .