湖南省郴州市2023-2024学年九年级上学期期末质量监测数学试卷
试卷更新日期:2024-02-01 类型:期末考试
一、选择题(共10个小题,每小题3分,共30分)
-
1. 在双曲线的每一支上,y随x的增大而增大,则k的值可以是( )A、2 B、0 C、-2 D、12. 某校七年级共有1200人,为了解这些学生的视力情况,随机抽查了20名学生的视力,对所得数据进行整理.若数据在4.85~5.15这一小组的频率为0.3,则可估计该校七年级学生视力在4.85~5.15范围内的人数有( )A、600人 B、360人 C、120人 D、60人3. 下列一元二次方程中,有实数根的方程是( )A、 B、 C、 D、4. 在中, , 则cosA的值是( )A、 B、 C、 D、5. 已知二次函数 , 下列说法正确的是( )A、顶点坐标为(2,-3) B、对称轴为 C、函数的最小值是-3 D、当 时 随x的增大而减小6. 为贯彻落实“绿水青山就是金山银山”的发展理念,某市大力开展植树造林活动.如图,在坡度 的山坡AB上植树,要求相邻两树间的水平距离AC为m,则斜坡上相邻两树间的坡面距离AB为( )
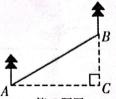 A、m B、4m C、3m D、7. 二次函数的图象如图所示,下列结论中错误的是( )
A、m B、4m C、3m D、7. 二次函数的图象如图所示,下列结论中错误的是( )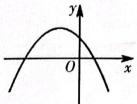 A、 B、b>0 C、c>0 D、8. 已知点 A(-2,y1),B(-1,y2),C(3,y3) 均在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 如图,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于点E,对角线BD交AG于点F.已知 , 则线段AE的长度为( )
A、 B、b>0 C、c>0 D、8. 已知点 A(-2,y1),B(-1,y2),C(3,y3) 均在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 如图,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于点E,对角线BD交AG于点F.已知 , 则线段AE的长度为( ) A、6 B、8 C、10 D、1210. 如图所示,在ΔABC中,点D为BC上的点,点F是AD的中点,连接BF并延长交AC于点E.已知 ,则( )
A、6 B、8 C、10 D、1210. 如图所示,在ΔABC中,点D为BC上的点,点F是AD的中点,连接BF并延长交AC于点E.已知 ,则( )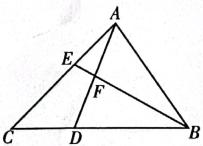 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共6个小题,每小题3分,共18分)
-
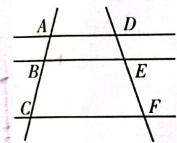
11. 已知 ,则的值为12. 如图, , 且 , BC=6cm,DF=15cm,则cm.
 13. 将抛物线 先向左平移2个单位,再向下平移2个单位,得到抛物线的表达式为14. 已知方程 可配方成 , 则15. 如图,在每个小正方形的边长为1的网格中,ΔABC的顶点A、B、C均落在格点上,则
13. 将抛物线 先向左平移2个单位,再向下平移2个单位,得到抛物线的表达式为14. 已知方程 可配方成 , 则15. 如图,在每个小正方形的边长为1的网格中,ΔABC的顶点A、B、C均落在格点上,则 16. 如图,在中,.反比例函数 )的图象分别过A,B两点.若 ,则k的值是 。
16. 如图,在中,.反比例函数 )的图象分别过A,B两点.若 ,则k的值是 。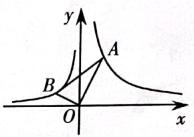
三、解答题(本大题共9个小题,第17-19题每题6分,第20-23题每题8分,第24-25题每题11分,共72分.解答应写出必要的文字说明、证明过程或演算步骤)
-
17. 解方程:18. 如图,已知直线与反比例函数 的图象相交于点A(2,a),与x轴相交于点B.
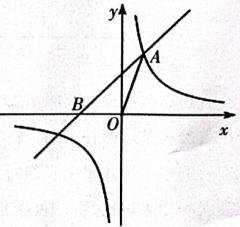 (1)、求反比例函数的表达式;(2)、求ΔAOB的面积.19. 如图,在平面直角坐标系中, BC三个顶点分别为
(1)、求反比例函数的表达式;(2)、求ΔAOB的面积.19. 如图,在平面直角坐标系中, BC三个顶点分别为 (1)、以坐标原点O为位似中心,位似比为 , 将ΔABC作位似变换后得到 , 请在平面直角坐标系中画出(2)、设ΔABC与C'面积分别为和 , 试求的值20. 某中学开展主题为“垃圾分类,绿色生活”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校团委在校园内随机抽取了部分学生进行问卷调查,将他们的得分按A:优秀,B:良好,C:合格,D:不合格四个等级进行统计,并绘制了如下不完整的条形统计图和扇形统计图.
(1)、以坐标原点O为位似中心,位似比为 , 将ΔABC作位似变换后得到 , 请在平面直角坐标系中画出(2)、设ΔABC与C'面积分别为和 , 试求的值20. 某中学开展主题为“垃圾分类,绿色生活”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校团委在校园内随机抽取了部分学生进行问卷调查,将他们的得分按A:优秀,B:良好,C:合格,D:不合格四个等级进行统计,并绘制了如下不完整的条形统计图和扇形统计图.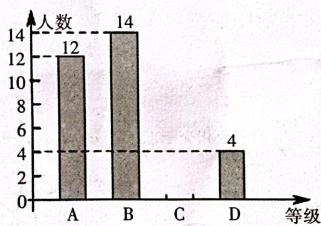
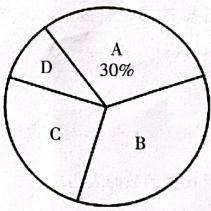 (1)、这次学校抽查的学生人数是(2)、将条形图补充完整;(3)、扇形统计图中C组对应的扇形圆心角度数是度;(4)、如果该校共有1800人,请估计该校不合格的人数.21. 某公园内建了一座纪念塔,纪念塔庄严肃穆,雄伟壮观.某数学活动小组欲测量纪念塔AB的高度.如图,他们选取的测量点D、C与纪念塔的底部B在同一水平线上.在D处测得纪念塔顶部A的仰角为30°,向前走20.6米到达C处,在C处测得纪念塔顶部A的仰角为45°,求纪念塔AB的高度(结果精确到0.1m.参考数据:
(1)、这次学校抽查的学生人数是(2)、将条形图补充完整;(3)、扇形统计图中C组对应的扇形圆心角度数是度;(4)、如果该校共有1800人,请估计该校不合格的人数.21. 某公园内建了一座纪念塔,纪念塔庄严肃穆,雄伟壮观.某数学活动小组欲测量纪念塔AB的高度.如图,他们选取的测量点D、C与纪念塔的底部B在同一水平线上.在D处测得纪念塔顶部A的仰角为30°,向前走20.6米到达C处,在C处测得纪念塔顶部A的仰角为45°,求纪念塔AB的高度(结果精确到0.1m.参考数据: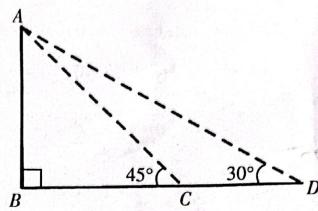 22. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆256人次,进馆人次逐月增加,第三个月进馆达到576人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过1000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次?并说明理由.23. 已知关于x的一元二次方程(1)、求证:不论k为何值时,此方程总有两个实数根;(2)、当方程的一个根为 时,求方程的另一个根x2及k的值.24. 如图,在RtΔABC中,.点D为线段AC上一动点(不与点A,C重合),把线段BD绕点B顺时针旋转90°后并延长为原来的2倍得到线段BF,连接CF,DF.
22. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆256人次,进馆人次逐月增加,第三个月进馆达到576人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过1000人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次?并说明理由.23. 已知关于x的一元二次方程(1)、求证:不论k为何值时,此方程总有两个实数根;(2)、当方程的一个根为 时,求方程的另一个根x2及k的值.24. 如图,在RtΔABC中,.点D为线段AC上一动点(不与点A,C重合),把线段BD绕点B顺时针旋转90°后并延长为原来的2倍得到线段BF,连接CF,DF.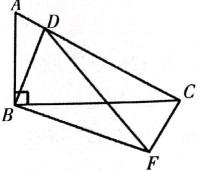 (1)、求证:(2)、求证:CF⊥AC;(3)、已知 , 设 , 在点D的运动过程中,ΔCDF的面积S是否存在最大值?若存在,求出最大值;若不存在,请说明理由.25. 抛物线 与x轴交于 B(1,0),C(-3,0)两点, 与y轴交于A点.
(1)、求证:(2)、求证:CF⊥AC;(3)、已知 , 设 , 在点D的运动过程中,ΔCDF的面积S是否存在最大值?若存在,求出最大值;若不存在,请说明理由.25. 抛物线 与x轴交于 B(1,0),C(-3,0)两点, 与y轴交于A点.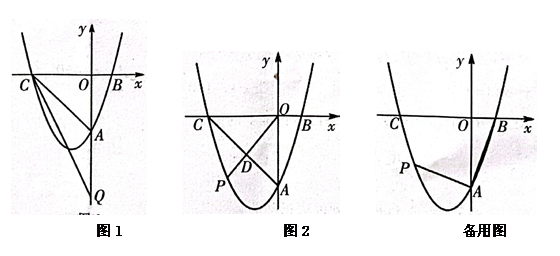 (1)、求抛物线的表达式;(2)、如图1,连接AC,在y轴的负半轴是否存在点Q,使得若存在,求Q点的坐标;若不存在,请说明理由.(3)、如图2,点P是抛物线上的一个动点,且点P在第三象限内,
(1)、求抛物线的表达式;(2)、如图1,连接AC,在y轴的负半轴是否存在点Q,使得若存在,求Q点的坐标;若不存在,请说明理由.(3)、如图2,点P是抛物线上的一个动点,且点P在第三象限内,①连接PO与直线AC交于点D,求的最大值;
②过点P作y轴的垂线交y轴于点M,若ΔABO~ΔPAM,求此时点P的横坐标.