浙江省嘉兴市重点中学2023-2024学年高一上学期数学12月月考试卷
试卷更新日期:2024-02-01 类型:月考试卷
一、单选题(共8题,每题5分,共40分)
-
1. 设集合 , ,则 ( )A、 B、 C、 D、2. 等于( )A、 B、 C、 D、3. 下列函数中,既是偶函数又在上单调递减的是( )A、 B、 C、 D、4. 关于 的方程 的两根都大于2,则 的取值范围是( )A、 B、 C、 D、5. 已知 , 则( )A、 B、 C、 D、6. 已知函数(且)的图像如图所示,则以下说法正确的是( )
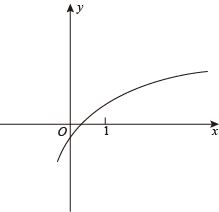 A、 B、 C、 D、7. 已知函数 ,若 在 上有且只有3个零点,则 的取值范围为( )A、 B、 C、 D、8. 已知为上的奇函数, , 若对 , , 当时,都有 , 则不等式的解集为( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知函数 ,若 在 上有且只有3个零点,则 的取值范围为( )A、 B、 C、 D、8. 已知为上的奇函数, , 若对 , , 当时,都有 , 则不等式的解集为( )A、 B、 C、 D、二、多选题(共4题,全部选对得5分,部分选对得2分,有选错的得0分,共20分)
-
9. 已知 , 则( )A、 B、 C、 D、10. 常见的《标准对数视力表》中有两列数据,分别表示五分记录数据和小数记录数据,把小数记录数据记为 , 对应的五分记录数据记为 , 现有两个函数模型:①;② . 根据如图所示的标准对数视力表中的数据,下列结论中正确的是( )
(参考数据:10-0.2≈0.6,10-0.15≈0.7,10-0.1≈0.8,10-0.05≈0.9)
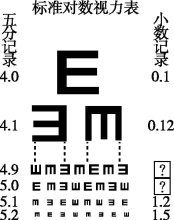 A、选择函数模型① B、选择函数模型② C、小明去检查视力,医生告诉他视力为 , 则小明视力的小数记录数据为 D、小明去检查视力,医生告诉他视力为 , 则小明视力的小数记录数据为11. 若 ,且 ,则下列不等式恒成立的是( )A、 B、 C、 D、12. 已知定义域为R的函数满足 , 函数 , 若函数为奇函数,则的值可以为( )A、 B、 C、π D、
A、选择函数模型① B、选择函数模型② C、小明去检查视力,医生告诉他视力为 , 则小明视力的小数记录数据为 D、小明去检查视力,医生告诉他视力为 , 则小明视力的小数记录数据为11. 若 ,且 ,则下列不等式恒成立的是( )A、 B、 C、 D、12. 已知定义域为R的函数满足 , 函数 , 若函数为奇函数,则的值可以为( )A、 B、 C、π D、三、填空题(共4题,每题5分,共20分)
-
13. .14. 已知 , 则 .15. 已知是上的奇函数,且对 , 有 , 当时, , 则 .16. 已知函数 , 若存在实数.满足 , 且 , 则 , 的取值范围是.
四、解答题(共6题,17题10分,其余各题12分,共70分)
-
17. 已知集合 , 集合(1)、若 , 求;(2)、若 , 求的取值范围.18. 已知 .(1)、若的终边位于第三象限角,求的值;(2)、求的值.19. 已知 , 角的顶点为坐标原点,始边与轴的非负半轴重合 , 终边经过点 , 且.求(1)、;(2)、.