贵州省部分重点中学2023-2024学年高三上学期数学1月模拟试卷
试卷更新日期:2024-02-01 类型:高考模拟
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
-
1. 已知集合 , , 则中元素的个数为( )A、0 B、1 C、2 D、无数个2. 设 , 则“”是“”的( )A、充要条件 B、既不充分也不必要条件 C、充分不必要条件 D、必要不充分条件3. 在的展开式中,含的系数为( )A、8 B、28 C、56 D、704. 如图,甲秀楼位于贵州省贵阳市南明区甲秀路,是该市的标志性建筑之一.甲秀楼始建于明朝,后楼毁重建,改名“凤来阁”,清代甲秀楼多次重修,并恢复原名、现存建筑是宣统元年(1909年)重建.甲秀楼上下三层,白石为栏,层层收进.某研究小组将测量甲秀楼最高点离地面的高度,选取了与该楼底在同一水平面内的两个测量基点与 , 现测得 , , , 在点测得甲秀楼顶端的仰角为 , 则甲秀楼的高度约为( )(参考数据: , )
 A、 B、 C、 D、5. 若数列满足 , 且 , 那么数列的前项和的最小值是( )A、 B、 C、 D、6. 已知函数( , , )的部分图象如图所示,则的对称中心为( )
A、 B、 C、 D、5. 若数列满足 , 且 , 那么数列的前项和的最小值是( )A、 B、 C、 D、6. 已知函数( , , )的部分图象如图所示,则的对称中心为( )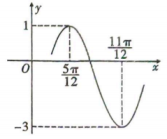 A、 B、 C、 D、7. 已知椭圆的左顶点为 , 上顶点为 , 右焦点为F , 的中点为M , , 则椭圆的离心率为( )A、 B、 C、 D、8. 已知是定义在上的奇函数,为偶函数,且在上单调递增,设 , , , 则a , b , c的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知椭圆的左顶点为 , 上顶点为 , 右焦点为F , 的中点为M , , 则椭圆的离心率为( )A、 B、 C、 D、8. 已知是定义在上的奇函数,为偶函数,且在上单调递增,设 , , , 则a , b , c的大小关系是( )A、 B、 C、 D、二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有错选的得0分)
-
9. 已知 , , 则下列结论正确的是( )A、 B、 C、与的夹角为 D、在方向上的投影向量是10. 定义:设是的导函数,是函数的导数,若方程有实数解 , 则称点为函数的“拐点”.经过探究发现:任何一个三次函数都有“拐点”且“拐点”就是三次函数图象的对称中心.已知函数图象的对称中心为 , 则下列说法中正确的有( )A、 , B、函数的极大值与极小值之和为2 C、函数有三个零点 D、在区间上单调递减11. 如图,四棱锥的底面为正方形,底面 , .设平面与平面的交线为 , 点为上的点,为上的点.下列说法正确的是( )
 A、平面 B、四棱锥外接球的半径为 C、点到的距离为. D、三棱锥的体积为12. 在中,内角A , B , C所对的边分别为a , b , c , 则下列说法正确的是( )A、若 , 且 , 则为直角三角形 B、若 , , , 要使满足条件的三角形有且只有两个,则 C、若平面内有一点满足: , 且 , 则为等边三角形 D、若 , 则为钝角三角形
A、平面 B、四棱锥外接球的半径为 C、点到的距离为. D、三棱锥的体积为12. 在中,内角A , B , C所对的边分别为a , b , c , 则下列说法正确的是( )A、若 , 且 , 则为直角三角形 B、若 , , , 要使满足条件的三角形有且只有两个,则 C、若平面内有一点满足: , 且 , 则为等边三角形 D、若 , 则为钝角三角形三、填空题(本大题共4小题,每小题5分,共20分)
-
13. 已知函数 , 则的最大值是.14. 拓扑结构图在计算机通信、计算机网络结构设计和网络维护等方面有着重要的作用.某树形拓扑结构图如图所示,圆圈代表节点,每一个节点都有两个子节点,则到第10层一共有个节点.(填写具体数字)
 15. 过点作曲线的切线,请写出切线的方程.16. 已知双曲线的左、右焦点分别为 , , 点在的左支上,过点作的一条渐近线的垂线,垂足为 , 则当取最小值16时,面积的最大值为.
15. 过点作曲线的切线,请写出切线的方程.16. 已知双曲线的左、右焦点分别为 , , 点在的左支上,过点作的一条渐近线的垂线,垂足为 , 则当取最小值16时,面积的最大值为.四、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)
-
17. 甲、乙、丙为完全相同的三个不透明盒子,盒内均装有除颜色外完全相同的球.甲盒装有4个白球,8个黑球,乙盒装有1个白球,5个黑球,丙盒装有3个白球,3个黑球.(1)、随机抽取一个盒子,再从该盒子中随机摸出1个球,求摸出的球是黑球的概率;(2)、已知(1)中摸出的球是黑球,求此球属于乙箱子的概率.18. 在中,内角A , B , C的对边分别为a , b , c , 且.(1)、求角的大小;(2)、若 , , 求边上的高.19. 如图,已知在四棱锥中,底面是矩形,平面底面 , , 是的中点.
 (1)、证明:;(2)、若 , , 求平面与平面的夹角的余弦值.20. 已知数列的前项和为 , 且.(1)、求数列的通项公式;(2)、在与之间插入个数,使这个数组成一个公差为的等差数列,在数列中是否存在3项 , , (其中p , m , q成等差数列)成等比数列?若存在,求出这样的3项;若不存在,请说明理由.
(1)、证明:;(2)、若 , , 求平面与平面的夹角的余弦值.20. 已知数列的前项和为 , 且.(1)、求数列的通项公式;(2)、在与之间插入个数,使这个数组成一个公差为的等差数列,在数列中是否存在3项 , , (其中p , m , q成等差数列)成等比数列?若存在,求出这样的3项;若不存在,请说明理由.