广东省六校2023-2024学年高一上学期数学期中联考试卷

试卷更新日期：2024-02-01 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $M = {- 1 ， 1 ， 2}$ ， $N = {x \in R | x^{2} = x}$ ，则 $M \cup N =$ （）

A、 ${1}$ B、 ${- 1 ， 0}$ C、 ${- 1 ， 0 ， 1 ， 2}$ D、 ${- 1 ， 0 ， 2}$

查看试题解析
2. 若非零实数 $a$ ， $b$ 满足 $| a | > | b |$ ，则下列不等式中一定成立的是（）

A、 $a - b > 0$ B、 $a^{2} - b^{2} > 0$ C、 $a^{3} - b^{3} > 0$ D、 $\frac{1}{a} < \frac{1}{b}$

查看试题解析
3. 已知函数 $y = f (x)$ 的定义域为 $[- 2 ， 3]$ ，则函数 $y = \frac{f (2 x + 1)}{x + 1}$ 的定义域为（）

A、 $[- \frac{3}{2} ， 1]$ B、 $[- \frac{3}{2} ， - 1) \cup (- 1 ， 1]$ C、 $[- 3 ， 7]$ D、 $[- 3 ， - 1) \cup (- 1 ， 7]$

查看试题解析
4. 设 $f (x)$ 是定义域为R的奇函数，且 $f (1 + x) = f (- x)$ .若 $f (- \frac{1}{3}) = \frac{1}{3}$ ，则 $f (\frac{5}{3}) =$ （）

A、 $- \frac{5}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、 $\frac{5}{3}$

查看试题解析
5. 已知函数 $y = (2 m - 1) x^{m} + n - 2$ 是幂函数，一次函数 $y = k x + b (k > 0 ， b > 0)$ 的图像过点 $(m ， n)$ ，则 $\frac{4}{k} + \frac{1}{b}$ 的最小值是（）

A、3 B、 $\frac{9}{2}$ C、 $\frac{14}{3}$ D、5

查看试题解析
6. “ $a \in (- \frac{1}{3} ， 3]$ ”是“函数 $f (x) = {\begin{array}{l} x^{2} - (a - 1) x + 2 ， x \geq 1 \\ (3 a + 1) x - 5 ， x < 1 \end{array}$ 是定义在 $R$ 上的增函数”的（）

A、必要不充分条件 B、充分不必要条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
7. 新型冠状病毒导致的疫情还没有完全解除．为了做好校园防技工作，某学校决定每天对教室进行消毒，已知消毒药物在释放过程中，室内空气中的含药量y（单位： $m g / m^{3}$ ）与时间t（单位：小时）成正比 $(0 < t < \frac{1}{2})$ ．药物释放完毕后，y与t的函数关系式为 $y = {(\frac{1}{4})}^{t - a}$ （a为常数， $t \geq \frac{1}{2}$ ）．按照规定，当空气中每立方米的含药量降低到 $0.5 m g / m^{3}$ 以下时，学生方可进入教室．因此，每天进行消毒的工作人员应当提前多长时间进行教室消毒？（）

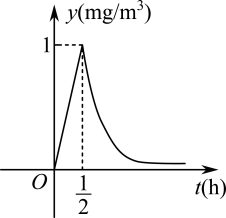A、30分钟 B、60分钟 C、90分钟 D、120分钟

查看试题解析
8. 已知函数 $f (x) = e^{x} + e^{- x} + l g | x |$ ，则不等式 $f (x + 1) > f (2 x - 1)$ 的解集为（）

A、 $(0 ， 2)$ B、 $(0 ， \frac{1}{2}) ∪ (\frac{1}{2} ， 2)$ C、 $(0 ， 3)$ D、 $(0 ， \frac{1}{2}) ∪ (\frac{1}{2} ， 3)$

查看试题解析

二、多选题

9. 下列说法正确的有（）

A、“ $\exists x_{0} \in R$ ， $2^{x_{0}} > x_{0}^{2}$ ”的否定是“ $\forall x \in R$ ， $2^{x} \leq x^{2}$ ” B、若命题“ $\exists x \in R$ ， $x^{2} + 4 x + m = 0$ ”为假命题，则实数 $m$ 的取值范围是 $(4 ， + \infty)$ C、若 $a$ ， $b$ ， $c \in R$ ，则“ $a b^{2} > c b^{2}$ ”的充要条件是“ $a > c$ ” D、“ $a > 1$ ”是“ $\frac{1}{a} < 1$ ”的充分不必要条件

查看试题解析
10. 下列说法正确的有（）

A、若 $f (x + 1) = x^{2} + x$ ，则 $f (0) = 2$ B、奇函数 $f (x)$ 和偶函数 $g (x)$ 的定义域都为R，则函数 $h (x) = f (x) g (x)$ 为奇函数 C、不等式 $k x^{2} + 2 k x - k - 2 < 0$ 对 $\forall x$ 恒成立，则实数k的取值范围是 $(- 1 ， 0)$ D、若 $\exists x \in R$ ，使得 $\frac{4 x + m}{x^{2} - 2 x + 3} \geq 2$ 成立，则实数m的取值范围是 $m \geq - 2$

查看试题解析
11. 已知 $x > 0$ ， $y > 0$ ，且 $x + 2 y = 1$ ，下列结论中正确的是（）

A、 $x y$ 的最小值是 $\frac{1}{8}$ B、 $2^{x} + 4^{y}$ 的最小值是 $2 \sqrt{2}$ C、 $\frac{1}{x} + \frac{2}{y}$ 的最小值是9 D、 $x^{2} + y^{2}$ 的最小值是 $\frac{2}{5}$

查看试题解析
12. 函数 $y = f (x)$ 图像关于坐标原点成中心对称图形的充要条件是函数 $y = f (x)$ 为奇函数，有同学据此推出以下结论，其中正确的是（）

A、函数 $y = f (x)$ 的图像关于点 $P (a ， b)$ 成中心对称的图形的充要条件是 $y = f (x + a) - b$ 为奇函数 B、函数 $f (x) = x^{3} - 3 x^{2}$ 的图像的对称中心为 $(1 ， - 2)$ C、函数 $y = f (x)$ 的图像关于 $x = a$ 成轴对称的充要条件是函数 $y = f (x - a)$ 是偶函数 D、函数 $g (x) = | x^{3} - 3 x^{2} + 2 |$ 的图像关于直线 $x = 1$ 对称

查看试题解析

三、填空题

13. 定义在 $R$ 上的函数 $f (x)$ ，当 $- 1 \leq x \leq 1$ 时， $f (x) = x^{3}$ ．若函数 $f (x + 1)$ 为偶函数，则 $f (3) =$ ．

查看试题解析
14. 方程 $x^{2} - (2 - a) x + 5 + a = 0$ 的一根大于1，一根小于1，则实数 $a$ 的取值范围是.

查看试题解析
15. 已知函数 $f (x) = x^{2} + 2 x + 1 + m$ ，若 $f (f (x)) \geq 0$ 恒成立，则实数m的最小值是.

查看试题解析
16. 若对任意 $x \geq 0$ ， $k \sqrt{1 + x} ⩾ 1 + \sqrt{x}$ 恒成立，则实数 $k$ 的取值范围是.

查看试题解析

四、解答题

17. 已知集合 $A = {x | a - 2 \leq x \leq 2 + a} (a \in R)$ ， $B = {x | \frac{1}{4} < 2^{x - 1} < 2}$ ．

(1)、当 $a = 3$ 时，求 $A \cup B$ ， $A ∩ (∁_{R} B)$ ；

(2)、若 $A ∪ (∁_{R} B) = R$ ，求实数 $a$ 的取值范围．

查看试题解析
18.

(1)、计算： ${(2 \frac{1}{4})}^{0.5} - 0.7 5^{2} + 6^{- 2} \times {(\frac{8}{27})}^{- \frac{2}{3}}$ ；

(2)、已知 $a^{\frac{1}{2}} + a^{- \frac{1}{2}} = 3$ ，求 $\frac{a^{3} + a^{- 3} + 3}{a + a^{- 1} - 2}$ 的值．

查看试题解析
19. 已知函数 $f (x) = \frac{3^{x} - a}{3^{x} + 1}$ 为奇函数.

(1)、求实数 $a$ 的值；

(2)、判断 $f (x)$ 在 $R$ 上的单调性（不必证明）；

(3)、解关于 $t$ 的不等式 $f (t^{2} - 2 t) + f (2 t^{2} - 1) < 0$ .

查看试题解析
20. 已知某种稀有矿石的价值（单位：元）与其重量（单位：克）的平方成正比，对该种矿石加工时，有时需要将一块较大的矿石切割成两块较小的矿石，在切割过程中的重量损耗忽略不计，但矿石的价值会损失.

(1)、把一块该种矿石切割成重量比为 $x ： 1$ 的两块矿石时，价值损失率为37.5%，求x的值；

(2)、把一块该种矿石切割成两块矿石时，价值损失率最大值是多少？
（注：价值损失率= $\frac{原有价值 - 现有价值}{原有价值} \times 100 %$ ）

查看试题解析
21. 已知函数 $f (x) = x^{2} - x$ ， $g (x) = 2 x - 2$ .

(1)、若 $\forall x_{1} \in [0 ， 3]$ ， $\exists x_{2} \in [0 ， 3]$ 使得 $f (x_{1}) + m \leq g (x_{2})$ 成立，求实数 $m$ 的取值范围；

(2)、当 $a \neq 0$ 时，解关于 $x$ 的不等式 $a f (x) > g (x)$ .

查看试题解析
22. 定义在 $R$ 上的奇函数 $f (x) = {\begin{array}{l} x ， - 1 < x < 0 ， \\ - a^{- x} ， x \leq - 1 ， \end{array}$ 其中 $a > 0 ， a \neq 1$ ，且 $f (1) = e$ ，其中 $e$ 是自然对数的底数， $e = 2.71828 ⋯$ .

(1)、当 $x \geq 0$ 时，求函数 $f (x)$ 的解析式；

(2)、若存在 $x_{2} > x_{1} \geq 0$ ，满足 $f (x_{2}) = e f (x_{1})$ ，求 $x_{1} \cdot f (x_{2})$ 的取值范围.

查看试题解析