湖南省怀化市八县九校2023-2024学年七年级上学期期末联考数学试题
试卷更新日期:2024-01-31 类型:期末考试
一、单选题(每小题3分,共30分)
-
1. -5的相反数是( )A、 B、 C、5 D、-52. 华为手机搭载了海思麒麟八核处理器,预装华为自主研发的操作系统,为全球首款支持卫星通话的智能手机.预计至2024年底,这款手机的出货量将达到70000000台.将70000000用科学记数法表示应为( )
 A、 B、 C、 D、3. 如图所示的平面图形绕直线l旋转一周,得到的立体图形是( )
A、 B、 C、 D、3. 如图所示的平面图形绕直线l旋转一周,得到的立体图形是( ) A、
A、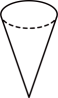 B、
B、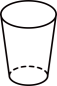 C、
C、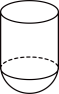 D、
D、 4. 若关于的一元一次方程的解为 , 则的值是( )A、 B、1 C、2 D、5. 下列说法正确的是( )A、的系数是 B、是单项式 C、的次数是8 D、是二次三项式6. 如图,两块直角三角板顶点重合, , 则重合部分的角度是( ).
4. 若关于的一元一次方程的解为 , 则的值是( )A、 B、1 C、2 D、5. 下列说法正确的是( )A、的系数是 B、是单项式 C、的次数是8 D、是二次三项式6. 如图,两块直角三角板顶点重合, , 则重合部分的角度是( ). A、 B、 C、 D、7. 以下问题.不适合用全面调查的是( )A、了解全班同学每周体育锻炼的时间 B、学校招聘老师,对应聘者进行面试 C、了解“神舟十五号”载人飞船发射前零部件的状况 D、某批种子的发芽率8. 某商品的标价为200元,8折销售仍赚40元,则商品进价为( )元.A、140 B、120 C、160 D、1009. 已知直线上 , 两点相距 , 点是线段的中点,点与点相距 , 则的长度是( )
A、 B、 C、 D、7. 以下问题.不适合用全面调查的是( )A、了解全班同学每周体育锻炼的时间 B、学校招聘老师,对应聘者进行面试 C、了解“神舟十五号”载人飞船发射前零部件的状况 D、某批种子的发芽率8. 某商品的标价为200元,8折销售仍赚40元,则商品进价为( )元.A、140 B、120 C、160 D、1009. 已知直线上 , 两点相距 , 点是线段的中点,点与点相距 , 则的长度是( ) A、 B、 C、 D、或10. 规定 . 如: , , 下列结论中:①若 , 则;②若 , 则;③当时,有最大值5;④式子的最小值是5,以上结论正确的为( )A、② B、②③④ C、①④ D、①②④
A、 B、 C、 D、或10. 规定 . 如: , , 下列结论中:①若 , 则;②若 , 则;③当时,有最大值5;④式子的最小值是5,以上结论正确的为( )A、② B、②③④ C、①④ D、①②④二、填空题(每小题3分,共18分)
-
11. 比较:(用 , , 填空)12. 已知的余角为 , 则 .13. 代数式与是同类项,则常数n的值为 .14. 一个正方体的表面展开图如图所示,六个面上各有一字,连起来的意思是“全面落实双减”,把它折成正方体后,与“面”相对的字是 .
 15. 已知 , 则代数式 .16. 把一根起点为0的数轴弯折成如图所示的样子,虚线最下面第1个数字是0,往上第2个数字是6,第3个数字是21,…,则第23个数字是 .
15. 已知 , 则代数式 .16. 把一根起点为0的数轴弯折成如图所示的样子,虚线最下面第1个数字是0,往上第2个数字是6,第3个数字是21,…,则第23个数字是 .
三、解答题(共9小题,共72分)
-
17. 计算:(1)、;(2)、 .18. 解方程:(1)、;(2)、 .19. 若(1)、请计算:;(2)、求当时,的值.20. 某中学积极倡导阳光体育运动,开展了排球垫球比赛,下表为七年级某班45人参加排球垫球山赛的情况,标准为每人垫球25个.
垫球个数与标准数量的差值
0
8
10
12
人数
5
10
10
5
10
5
(1)、求这个班45人平均每人垫球多少个;(2)、规定垫球达到标准数量记0分,超过标准数量,每多垫1个加2分;未达到标准数量,每少垫1个扣1分,求这个班垫球总共获得多少分.21. 某校兴趣小组以网络问卷调查的形式,随机调查了某地居民对“中国第三次成功承办亚运会"的原因认识情况,设置了单选题,并将调查结果绘制成如下不完整的统计图.选项
A
B
C
D
E
“中国第三次成功承办亚运会”的原因
经济持续稳定快速发展
中国特色社会主义制度
志愿者们的无私奉献
社会主义制度的优越性
构建人类命运共同体思想
根据以上信息回答下列问题:
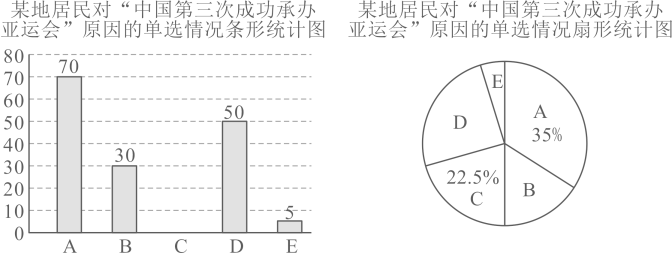 (1)、求本次调查的总人数,并补全条形统计图(要求标注人数).(2)、在扇形统计图中,求E选项对应圆心角的度数.(3)、在该地100万居民中,估计有多少居民认为中国第三次成功承办亚运会得益于构建人类命运共同体思想?22. 如图,已知是直角, , 平分 .
(1)、求本次调查的总人数,并补全条形统计图(要求标注人数).(2)、在扇形统计图中,求E选项对应圆心角的度数.(3)、在该地100万居民中,估计有多少居民认为中国第三次成功承办亚运会得益于构建人类命运共同体思想?22. 如图,已知是直角, , 平分 .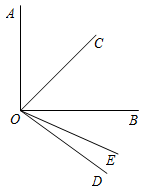 (1)、求的度数;(2)、求的度数.23. 某工厂现有木料,准备制作圆桌或方桌,用部分木料制作桌面,其余木料制作桌腿.(1)、已知一张圆桌由一个桌面和一条桌腿组成,木料可制作40个桌面或制作20条桌腿.要使制作出的桌面、桌腿恰好配套,则制作桌面的木料为多少?(2)、已知一张方桌由一个桌面和四条桌腿组成.如果木料可制作50个桌面或制作300条桌腿,应怎样计划用料才能使做好的桌面和桌腿恰好配套?24. 下表是2023年10月的月历,观察月历,回答问题:
(1)、求的度数;(2)、求的度数.23. 某工厂现有木料,准备制作圆桌或方桌,用部分木料制作桌面,其余木料制作桌腿.(1)、已知一张圆桌由一个桌面和一条桌腿组成,木料可制作40个桌面或制作20条桌腿.要使制作出的桌面、桌腿恰好配套,则制作桌面的木料为多少?(2)、已知一张方桌由一个桌面和四条桌腿组成.如果木料可制作50个桌面或制作300条桌腿,应怎样计划用料才能使做好的桌面和桌腿恰好配套?24. 下表是2023年10月的月历,观察月历,回答问题:星期日
星期一
星期二
星期三
星期四
星期五
星期六
1休(阴影)
2休(阴影)
3休
4休
5休
6休
7
8(阴影)
9(阴影)
10
11
12
13
14
15
16
17
18
19(阴影)
20
21
22
23
24
25(阴影)
26(阴影)
27
28
29
30
31
(1)、小欢国庆假期外出旅行三天,三天日期之和是12,小欢是星期几出发的?(2)、“J 型”、“田型”两个阴影图形分别覆盖其中三、四个方格(可以重叠覆盖),设“J 型” 阴影覆盖的最小数字为 , 三个数字之和为 , “田型”阴影覆盖的最小数字为 , 四个数字之和为 .①2023年是建国74周年,的值能否等于74?若能,求出的值;若不能,说明理由;
②的值能否等于74?若能,求出的所有值;若不能,说明理由 .
25. 如图,数轴上A,B两点表示的有理数分别为a、b,满足 , 原点O是线段AB上的一点. (1)、a= , b= , AB= ;(2)、若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当t为何值时,BP=2BQ?(3)、若点P、Q仍按(2)中速度运动,当点P与点Q重合时停止运动,当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中M点行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.
(1)、a= , b= , AB= ;(2)、若动点P,Q分别从A,B同时出发,向右运动,点P的速度为每秒2个单位长度,点Q的速度为每秒1个单位长度,设运动时间为t秒,当t为何值时,BP=2BQ?(3)、若点P、Q仍按(2)中速度运动,当点P与点Q重合时停止运动,当点P到达点O时,动点M从点O出发,以每秒3个单位长度的速度也向右运动,当点M追上点Q后立即返回,以同样的速度向点P运动,遇到点P后再立即返回,以同样的速度向点Q运动,如此往返,直到点P,Q停止时,点M也停止运动,求在此过程中M点行驶的总路程,并直接写出点M最后位置在数轴上所对应的有理数.