浙江省杭州市拱墅区2023-2024学年七年级上学期数学期末学情调研试卷
试卷更新日期:2024-01-30 类型:期末考试
一、选择题(10小题,每小题3分,共30分)
-
1. 的倒数是( )A、 B、2023 C、 D、2. 杭州奥体中心体育馆是第19届杭州亚运会开闭幕式主会场,其建筑面积约为74470平方米,数据74470用科学记数法表示为( )A、 B、 C、 D、744.73. 下列说法正确的是( )A、4的平方根是2 B、8的立方根是±2 C、3 D、没有平方根4. 下列说法正确的是( )A、两点之间直线最短 B、如果=53 , 那么的补角的度数为37 C、如果一个角的余角和补角都存在,那么这个角的余角比这个角的补角小 D、相等的两个角是对顶角5. 下列说法正确的是( )A、与的和为0 B、是三次三项式 C、的系数是 , 次数是4次 D、与不是同类项6. 一副三角板按如图方式摆放,且比大 , 则的度数是( )
 A、 B、 C、 D、7. 程大位《算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分一个,正好分完.试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、3x+=100 B、3x﹣=100 C、 D、8. 如图,点O在直线AB上,OC⊥AB,OE⊥OF,若∠AOE=45.2°,则∠COF=( )
A、 B、 C、 D、7. 程大位《算法统宗》:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分一个,正好分完.试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、3x+=100 B、3x﹣=100 C、 D、8. 如图,点O在直线AB上,OC⊥AB,OE⊥OF,若∠AOE=45.2°,则∠COF=( ) A、45°12´ B、45°20´ C、44°48´ D、44°80´9. 三张大小不一的正方形纸片按如图1和图2方式分别放置于相同的长方形中,它们既不重叠也无空隙,记图1阴影部分周长之和为m , 图2阴影部分周长为n , 要求m与n的差,只需知道一个图形的边长,这个图形是( )
A、45°12´ B、45°20´ C、44°48´ D、44°80´9. 三张大小不一的正方形纸片按如图1和图2方式分别放置于相同的长方形中,它们既不重叠也无空隙,记图1阴影部分周长之和为m , 图2阴影部分周长为n , 要求m与n的差,只需知道一个图形的边长,这个图形是( ) A、整个长方形 B、图①正方形 C、图②正方形 D、图③正方形10. 已知关于x的一元一次方程的解是 , 关于y的一元一次方程的解是(其中b和c是含有y的代数式),则下列结论符合条件的是( )A、 B、 C、 D、
A、整个长方形 B、图①正方形 C、图②正方形 D、图③正方形10. 已知关于x的一元一次方程的解是 , 关于y的一元一次方程的解是(其中b和c是含有y的代数式),则下列结论符合条件的是( )A、 B、 C、 D、二、填空题(6小题,每小题4分,共24分)
-
11. 一个数具有以下两个特点:①它的绝对值等于3;②它是负数.这个数是.12. 某粮店出售的两种品牌的面粉袋上分别标有质量为(25±0.1)kg,(25±0.2)kg的字样,从中任意拿出两袋,它们的质量最多相差kg.13. 如果代数式的值为3,那么代数式:的值等于 .14. 如图:已知∠AOB=60°,OC平分∠A0B,在同一平面内以O为端点画射线OD,使∠COD=10°,则∠AOD=.
 15. 有两所图书馆,自建馆以来每年各进图书0.5万册,若今年甲馆共有藏书27万册,乙馆共有藏书11万册,从今年起,n年后甲馆的藏书是乙馆的2倍,则n=.16. 如图,C是线段AB上的一点,D是BC中点,已知图中所有线段长度之和为23.
15. 有两所图书馆,自建馆以来每年各进图书0.5万册,若今年甲馆共有藏书27万册,乙馆共有藏书11万册,从今年起,n年后甲馆的藏书是乙馆的2倍,则n=.16. 如图,C是线段AB上的一点,D是BC中点,已知图中所有线段长度之和为23. (1)、设线段BD的长为x , 则线段AC= . (用含x的代数式表示).(2)、若线段AC , BD的长度都是正整数,则线段AC的长为 .
(1)、设线段BD的长为x , 则线段AC= . (用含x的代数式表示).(2)、若线段AC , BD的长度都是正整数,则线段AC的长为 .三、解答题(8小题,共66分)
-
17. 计算:(1)、(2)、(3)、 .18. 解方程:(1)、(2)、-19. 如图,线段 , 是线段上一点, , 、分别是、的中点.
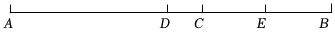 (1)、求线段的长;
(1)、求线段的长;
(2)、求线段的长.20. 已知x-6和3x+14是a的两个不同的平方根,2y-6是a的立方根.(1)、求x,y,a的值.(2)、求-7-4y的立方根.21. 已知代数式A=(1)、求;(2)、当x=﹣1,y=2时,求的值.(3)、若的值与x的取值无关,求y的值.22. 某校开展劳动教育,在植树节当天组织植树活动,该校七年级共有120人参加活动,分成树苗保障组和种植组,种植组的人数是树苗保障组人数的2倍.(1)、求树苗保障组的人数;(2)、已知种植点有甲、乙两处,种植组在甲处有人.①用含的代数式表示种植组在乙处的人数;
②若 , 树苗保障组人员在运送完树苗后全部去支援种植组,使在甲处种植的人数是乙处种植人数的2倍,问应调往甲、乙两处各多少人?
23. 一副三角板如图放置,其中有部分重叠在一起,已知 (1)、若 , 求的度数;(2)、若 , 求的度数;(3)、若 , 其中0 , 求的度数.(用含k的代数式表示)24. 如图,在数轴上A点表示的数 , B点表示的数,C点表示的数,是最小的正整数,且 , 满足+=0
(1)、若 , 求的度数;(2)、若 , 求的度数;(3)、若 , 其中0 , 求的度数.(用含k的代数式表示)24. 如图,在数轴上A点表示的数 , B点表示的数,C点表示的数,是最小的正整数,且 , 满足+=0 (1)、求= , = , c=;(2)、若将数轴折叠,使得A点与B点重合,则与C点重合的点对应的数是;(3)、若点A以每秒0.2个单位的速度向右运动,点C以每秒0.3个单位的速度向左运动,直至两点相遇时停止运动.
(1)、求= , = , c=;(2)、若将数轴折叠,使得A点与B点重合,则与C点重合的点对应的数是;(3)、若点A以每秒0.2个单位的速度向右运动,点C以每秒0.3个单位的速度向左运动,直至两点相遇时停止运动.①若两点同时开始运动,求相遇处的点所表示的数;
②若点A先运动秒后,点C开始运动,A,C两点恰好在点B处相遇,求的值;
③若两点同时开始运动,点C是否有可能比点A多运动1.5个单位?说明理由.