浙江省杭州市上城区2023-2024学年七年级上学期数学期末模拟卷

试卷更新日期：2024-01-30 类型：期末考试

进入出卷网下载

一、选择题（本大题有10个小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的）

1. -3的相反数是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 被英国《卫报》誉为“新世界七大奇迹”的港珠澳大桥是中国境内一座连接香港，广东珠海和澳门桥隧工程，它是世界上最长的跨海大桥，桥隧全长55000米，其中55000用科学记数法表示为（）

A、 $55 \times 1 0^{4}$ B、 $5.5 \times 1 0^{4}$ C、 $5.5 \times 1 0^{5}$ D、 $0.55 \times 1 0^{6}$

查看试题解析
3. 在实数 $- \sqrt{3} ， - 3.14 ， 0 ， π ， \sqrt[3]{64}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 四个互不相等的整数的积为49，则它们的和为（）

A、0 B、8 C、16 D、8或1

查看试题解析
5. 当 $a < 0$ 时，下列四个结论：① $a^{2} > 0$ ；② $a^{2} = {(- a)}^{2}$ ；③ $- a^{3} = | a^{3} |$ ；④ $- a^{2} = | - a^{2} |$ ，其中一定正确的有（）

A、 $1$ 个 B、 $2$ 个 C、3个 D、 $4$ 个

查看试题解析
6. 方程 $- 2 x = \frac{1}{2}$ 的解是（）

A、 $x = - \frac{1}{4}$ B、 $x = 4$ C、 $x = \frac{1}{4}$ D、 $x = - 4$

查看试题解析
7. 《增删算法统宗》记载：“有个学生资性好，一部孟子三日了，每日增法添一倍多，问君每日读多少？”其大意是：有个学生天资聪慧，三天读完一部《孟子》，每天阅读的字数是前一人的两倍．问他每天各读多少个子？已知《孟子》一书共有34685个字，设他第一天读 $x$ 个字，则下面所列方程正确的是（）

A、 $x + 2 x + 4 x = 34685$ B、 $x + 2 x + 3 x = 34685$ C、 $x + 2 x + 2 x = 34685$ D、 $x + \frac{1}{2} x + \frac{1}{4} x = 34685$

查看试题解析
8. $a$ 、 $b$ 在数轴上的位置如图所示，那么化简 $| a - b | - \sqrt{a^{2}}$ 的结果是（）

A、 $2 a - b$ B、 $b$ C、 $- b$ D、 $- 2 a + b$

查看试题解析
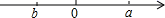9. 现定义一种新运算“※”，对任意有理数a、b，规定 $a$ ※ $b = a b + a - b$ ，例如：1※ $2 = 1 \times 2 + 1 - 2 = 1$ ，则2※ $(- 3)$ 等于（）

A、-3 B、-2 C、-1 D、0

查看试题解析
10. 已知： $m = \frac{| a + b |}{c} + \frac{2 | b + c |}{a} + \frac{3 | c + a |}{b}$ ，且abc＞0，a+b+c=0.则m共有x个不同的值，若在这些不同的m值中，最大的值为y，则x+y=（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题（本大题有6个小题,每小题4分,共24分）

11. 比较大小：4 $\sqrt{20}$ (填“>”“<”或“=”)。

查看试题解析
12. 若一个角的大小为 $35 ° 1 8^{'}$ ，则这个角的补角的大小为．

查看试题解析
13. 若代数式 $2 x^{2} + 3 x + 7$ 的值为8，则代数式 $4 x^{2} + 6 x - 9$ 的值是.

查看试题解析
14. 解一元一次方程 $\frac{1}{2} (x + 1) = 1 - \frac{1}{3} x$ 时，去分母后得到的方程是.

查看试题解析
15. 设有理数a，b，c满足a+b+c=0，abc> 0，则a，b，c中正数的个数为

查看试题解析
16. 一只昆虫从点 $A$ 处出发，以每分钟2米的速度在一条直线上运动，它先前进1米，再后退2米，又前进3米，再后退4米， $⋯$ 依此规律继续走下去，则运动1小时这只昆虫与 $A$ 点相距米.

查看试题解析

三、解答题（本大题有7小题，共66分，解答应写出文字说明、证明过程或演算步骤）

17. 解方程：

(1)、 $5 x + 2 = 3 (x + 2)$

(2)、 $\frac{x + 3}{6} = 1 - \frac{3 + 2 x}{4}$

查看试题解析
18. 先化简后求值： $3 a^{2} b - [a b^{2} - (- 2 a b^{2} + 5 a^{2} b)] - 2 (a^{2} b - a b^{2})$ ，其中 $a = - 1 ， b = - 2$ ．

查看试题解析
19.

(1)、在下面带有箭头的直线上先确定好原点以及单位长度，然后在所得的数轴上把下列各数表示出来： $- 2 ， 3.5 ， - 1 \frac{1}{2} ， 2.75 ， 2 \frac{1}{3} ， - 3$ .

(2)、将上面6个数用“<”连接起来

查看试题解析
20. 定义：如果两个一元一次方程的解之和为1，我们就称这两个方程为“和谐方程”．例如：方程 $4 x = 8$ 和 $x + 1 = 0$ 为“和谐方程”．

(1)、若关于x的方程 $3 x + m = 0$ 与方程 $4 x - 2 = x + 10$ 是“和谐方程”，求m的值；

(2)、若关于x的两个方程 $\frac{x}{3} + m = 0$ 与 $\frac{3 x - 2}{5} = \frac{x + m}{2}$ 是“和谐方程，求m的值．

查看试题解析
21. 第24届冬奥会于2022年2月4日在北京举行，某经销商在冬奥会前预测带有“冰墩墩”吉祥物标志的甲、乙两种纪念品可能会畅销，于是，该经销商用6 200元一次性购进了甲、乙两种纪念品共100件.已知甲、乙两种纪念品的进价和售价如表：
种类
进价(元/件)
售价(元/件)
甲
50
100
乙
70
90

(1)、该经销商一次性购进甲、乙两种纪念品各多少件?

(2)、如果在北京冬奥会开幕式当天销售完全部纪念品，则可获得利润为多少元?

(3)、根据预测的销售情况，该经销商会再次以相同的进价购进甲、乙两种纪念品，已知甲种纪念品的数量是第一次购进甲种纪念品数量的2倍，乙种纪念品的数量与第一次所购乙种纪念品数量相同.如果甲种纪念品打折销售，乙种纪念品按原价销售，全部销售完后所获的利润正好比第一次获得的利润多1 200元，则甲种纪念品应按原价打几折销售?

查看试题解析
22. 如图所示，点P是线段AB上任意一点，AB=12 cm，C，D两点分别从点P，B同时向点A运动，且点C的运动速度为2 cm/s，点D的运动速度为3 cm/s，运动时间为t s.

(1)、若AP=8 cm：
①两点运动1 s后，求CD的长；
②当点D在线段PB上运动时，试说明：AC=2CD；

(2)、当t=2时，CD=1 cm，试探索AP的长.

查看试题解析
23. 已知：射线OD在 $∠ A O B$ 内部， $O E 平分 ∠ A O D$ .

(1)、如图1，求证： $∠ A O B - ∠ E O B = ∠ D O E$ ；

(2)、如图2，作OF平分∠AOB，求证： $∠ E O F = \frac{1}{2} ∠ D O B$ ；

(3)、如图3，在（2）的条件下，当∠AOD=90°时，作射线OA的反向延长线OC，OH在OA的下方，且∠AOH=∠AOE，反向延长射线OE得到射线OQ，射线OP在∠HOQ内部，OG是∠EOP的平分线，若∠BOC-∠DOF=26°，5∠GOH-2∠POQ-∠EOF=71°，求∠BOP的度数.

查看试题解析

种类	进价(元/件)	售价(元/件)
甲	50	100
乙	70	90