广东省广州市2023-2024学年九年级（上）期末考试模拟卷

试卷更新日期：2024-01-30 类型：期末考试

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 下列与杭州亚运会有关的图案中，中心对称图形是（）

A、 B、 C、 D、

查看试题解析
2. 成语“水中捞月”所描述的事件是（）.

A、必然事件 B、随机事件 C、不可能事件 D、无法确定

查看试题解析
3. 用配方法解一元二次方程x²+4x﹣5=0，此方程可变形为（　　）

A、（x+2）²=9 B、（x﹣2）²=9 C、（x+2）²=1 D、（x﹣2）²=1

查看试题解析
4. 随机抛掷一枚瓶盖1000次，经过统计得到“正面朝上”的次数为420次，则可以由此估计抛掷这枚瓶盖出现“反面朝上”的概率为（）

A、0.22 B、0.42 C、0.50 D、0.58

查看试题解析
5. 如图，A、B、C是⊙O上的三个点，若∠B＝30°，则∠OAC的度数为（）

A、15° B、30° C、50° D、60°

查看试题解析
6. 如图，将△ABC绕点A顺时针旋转60°得到△AED ，若线段AB＝4，则BE的长为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 已知反比例函数y＝﹣ $\frac{2}{x}$ ，下列结论不正确的是（）

A、图象必经过点(﹣1，2) B、y随x的增大而增大 C、图象在第二、四象限内 D、若x＞1，则﹣2＜y＜0

查看试题解析
8. 若M（﹣4，y₁），N（﹣3，y₂），P（1，y₃）为二次函数y＝x²+4x﹣5的图象上的三点，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
9. 关于x的一元二次方程kx²+3x﹣1=0有实数根，则k的取值范围是（）

A、k≤﹣ $\frac{9}{4}$ B、k≤﹣ $\frac{9}{4}$ 且k≠0 C、k≥﹣ $\frac{9}{4}$ D、k≥﹣ $\frac{9}{4}$ 且k≠0

查看试题解析
10. 如图，抛物线y＝ax²+bx+c与x轴相交于点A（﹣2，0），B（6，0），与y轴相交于点C．小红同学得出了以下结论：①4ac＜b²；②4a+b＝0；③当y＞0时，﹣2＜x＜6；④关于x的方程ax²+bx+（c﹣2）＝0有两个不等实根；⑤对任意的实数m，am²﹣4a≥﹣bm+2b．其中正确的个数为（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题（共6小题，满分18分，每小题3分）

11. 点P（﹣1，3）关于原点对称的点的坐标是．

查看试题解析
12. 已知方程2x²﹣mx+3＝0的一个根是﹣1，则m的值是．

查看试题解析
13. 在一个不透明的袋子里装有红球和白球共30个，这些球除颜色外都相同，小明通过多次试验发现，摸出白球的频率稳定在0.3左右，则袋子里白球可能是个．

查看试题解析
14. 已知圆锥的母线长为8，底面半径为6，则此圆锥的侧面积是

查看试题解析
15. 已知二次函数的图象经过点 $P (2 ， 2)$ ，顶点为 $O (0 ， 0)$ 将该图象向右平移，当它再次经过点 $P$ 时，所得抛物线的函数表达式为.

查看试题解析
16. 如图，已知点A是反比例函数y= $\frac{10}{x}$ (x>0)的图象上一点，AB∥x轴交另一个反比例函数y= $\frac{k}{x}$ (x>0)的图象于点B，C为x轴上一点，若S_△ABC＝2，则k的值为．

查看试题解析

三、解答题（共9小题，满分72分）

17. 解方程：3x（2x﹣5）＝5（2x﹣5）．

查看试题解析
18. 如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（﹣1，5），B（﹣4，3），C（﹣2，2）．

(1)、画出与△ABC关于原点对称的△A₁B₁C₁；

(2)、画出将△ABC绕点O顺时针旋转90°后得到的△A₂B₂C₂ ，并写出B₂的坐标．

查看试题解析
19. 一根排水管的截面如图所示．已知水面宽AB＝8dm，测得排水管内水的最大深度为2dm，求排水管截面的半径．

查看试题解析
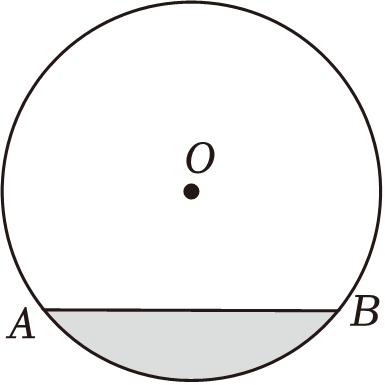20. 临近期末考试，心理专家建议考生可通过以下四种方式进行考前减压： $A$ .享受美食， $B$ .交流谈心， $C$ .体育锻炼， $D$ .欣赏艺术.

(1)、随机采访一名九年级考生，选择其中某一种方式，他选择“享受美食”的概率是.

(2)、同时采访两名九年级考生，请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.

查看试题解析
21. 某公司2月份销售新上市的A产品20套，由于该产品的经济适用性，销量快速.上升，4月份该公司销售A产品达到45套，并且2月到3月和3月到4月两次的增长率相同.

(1)、求该公司销售A产品每次的增长率；

(2)、若A产品每套盈利2万元，则平均每月可售30套，为了尽量减少库存，该公司决定采取适当的降价措施，经调查发现，A产品每套每降0.5万元，公司平均每月可多售出20套；若该公司在5月份要获利70万元，则每套A产品需降价多少?

查看试题解析
22. 已知一次函数y₁＝﹣x+7的图象与反比例函数y₂＝ $\frac{k}{x}$ 图象交于A、B两点，且A点的横坐标﹣1，求：

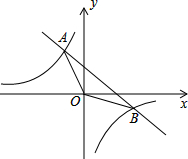(1)、反比例函数的解析式．

(2)、△AOB的面积．

(3)、直接写出满足y₁≤y₂时x的取值范围．

查看试题解析
23. 如图，在菱形ABCD中，AC为菱形的一条对角线，以AB为直径作⊙O，交AC于点E，交BC于点F，G为CD边上一点，且BF＝DG．

(1)、求证：AG为⊙O的切线；

(2)、若AE= $\frac{5}{2}$ ， CF＝3，求⊙O的半径．

查看试题解析
24. 如图，抛物线y＝ax²+bx﹣3与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C．

(1)、求抛物线的解析式；

(2)、若点D是抛物线上的一点，当△ABD的面积为10时，求点D的坐标；

(3)、点P是抛物线对称轴上的一点，在抛物线上是否存在一点Q，使得以B、C、P、Q为顶点的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析
25. 阅读下面材料，并解决问题：

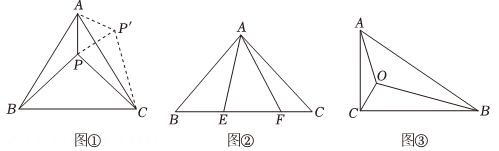(1)、如图①等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数．
为了解决本题，我们可以将△ABP绕顶点A旋转到△ACP^'处，此时△ACP^'≌△ABP，这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB＝ ▲ ；

(2)、基本运用
请你利用第（1）题的解答思想方法，解答下面问题
已知如图②，△ABC中，∠CAB＝90°，AB＝AC，E、F为BC上的点且∠EAF＝45°，求证：EF²＝BE²+FC²；

(3)、能力提升
如图③，在Rt△ABC中，∠C＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°，求OA+OB+OC的值．

查看试题解析