广东省惠州市2023-2024学年八年级(上)期末质量监测猜题卷
试卷更新日期:2024-01-30 类型:期末考试
一、选择题(共10小题,满分30分,每小题3分)
-
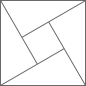
1. 下列图形中,为轴对称的图形的是( )A、
 B、
B、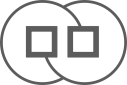 C、
C、 D、
D、 2. 已知某细菌直径长约0.0000152米,那么该细菌的直径长用科学记数法可表示为( )A、152×105米 B、1.52×10﹣5米 C、﹣1.52×105米 D、1.52×10﹣4米3. 下列长度的三条线段能组成三角形的是( )A、3cm , 5cm , 7cm B、3cm , 3cm , 7cm C、4cm , 4cm , 8cm D、4cm , 5cm , 9cm4. 下列计算,其中正确的是( )A、x3•x2=x6 B、(ab)6=ab6 C、(﹣a3)2=a6 D、3x3y2÷xy2=3x35. 如图,点E、点F在BC上,BE=CF, ∠B=∠C, 添加一个条件,不能证明△ABF≌△DCE的是( )
2. 已知某细菌直径长约0.0000152米,那么该细菌的直径长用科学记数法可表示为( )A、152×105米 B、1.52×10﹣5米 C、﹣1.52×105米 D、1.52×10﹣4米3. 下列长度的三条线段能组成三角形的是( )A、3cm , 5cm , 7cm B、3cm , 3cm , 7cm C、4cm , 4cm , 8cm D、4cm , 5cm , 9cm4. 下列计算,其中正确的是( )A、x3•x2=x6 B、(ab)6=ab6 C、(﹣a3)2=a6 D、3x3y2÷xy2=3x35. 如图,点E、点F在BC上,BE=CF, ∠B=∠C, 添加一个条件,不能证明△ABF≌△DCE的是( ) A、∠A=∠D B、∠AFB=∠DEC C、AB=DC D、AF=DE6. 下列等式中,从左到右的变形是因式分解的是( )A、x(x﹣2)=x2﹣2x B、(x+1)2=x2+2x+1 C、x+2=x(1+) D、x2﹣4=(x+2)(x﹣2)7. 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为16cm,则△ABC的周长是( )
A、∠A=∠D B、∠AFB=∠DEC C、AB=DC D、AF=DE6. 下列等式中,从左到右的变形是因式分解的是( )A、x(x﹣2)=x2﹣2x B、(x+1)2=x2+2x+1 C、x+2=x(1+) D、x2﹣4=(x+2)(x﹣2)7. 如图,在△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为16cm,则△ABC的周长是( ) A、20cm B、24cm C、26cm D、28cm8. 某校计划修建一条500米长的跑道,开工后每天比原计划多修15米,结果提前2天完成任务.如果设原计划每天修x米,那么根据题意可列出方程( )A、﹣=2 B、﹣=2 C、﹣=2 D、﹣=29. 如图,在中,已知点D、E,F分别为、、的中点,且 , 则阴影部分面积S=( ) .
A、20cm B、24cm C、26cm D、28cm8. 某校计划修建一条500米长的跑道,开工后每天比原计划多修15米,结果提前2天完成任务.如果设原计划每天修x米,那么根据题意可列出方程( )A、﹣=2 B、﹣=2 C、﹣=2 D、﹣=29. 如图,在中,已知点D、E,F分别为、、的中点,且 , 则阴影部分面积S=( ) . A、1 B、2 C、3 D、410. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )
A、1 B、2 C、3 D、410. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( ) A、(a+b)2=a2+2ab+b2 B、(a﹣b)2=a2﹣2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、(a+2b)(a﹣b)=a2+ab﹣2b2
A、(a+b)2=a2+2ab+b2 B、(a﹣b)2=a2﹣2ab+b2 C、a2﹣b2=(a+b)(a﹣b) D、(a+2b)(a﹣b)=a2+ab﹣2b2二、填空题(共6小题,满分18分,每小题3分)
-
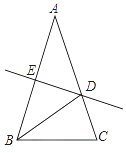
11. 若代数式有意义,则实数x的取值范围是 .12. 分解因式:3m3﹣12m= .13. 在平面直角坐标系中,点A(﹣5,2)关于y轴对称点B的坐标是 .14. 已知一多边形的内角和等于1440°,则这个多边形是 边形.15. 若x+m与x+7的乘积不含x的一次项,则m的值为 .16. 如图,在△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,(1)BD平分∠ABC;(2)点D是线段AC的中点;(3)AD=BD=BC;(4)△BDC的周长等于AB+BC,上述结论正确的是 .
三、解答题(共9小题,满分72分)
-
17. 计算: .18. 解分式方程: .19. 先化简,再求值:(2x﹣3y)2﹣(2x+y)(2x﹣y),其中x=﹣ , y=﹣2.20. 如图,在直角坐标系中, 的三个顶点坐标分别为A (1,4),B(4,2),C(3,5),请回答下列问题:
 (1)、写出 关于x轴的对称图形 的顶点坐标.(2)、求 的面积.21. 已知W=+ .(1)、化简W;(2)、若a,2,4恰好是等腰△ABC的三边长,求W的值.22. 已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M.
(1)、写出 关于x轴的对称图形 的顶点坐标.(2)、求 的面积.21. 已知W=+ .(1)、化简W;(2)、若a,2,4恰好是等腰△ABC的三边长,求W的值.22. 已知:如图,D为△ABC外角∠ACP平分线上一点,且DA=DB,DM⊥BP于点M. (1)、若AC=6,DM=2,求△ACD的面积;(2)、求证:AC=BM+CM.23. 戴口罩可以有效降低感染新型冠状病毒的风险.某学校在本学期开学初为八年级学生购买A、B两种口罩,经过市场调查,每包A口罩比每包B口罩少10元,花费400元购买A口罩和花费600元购买B口罩的数量相等.(1)、求A、B两种口罩每包的价格各是多少元?(2)、若学校需购买两种口罩共500包,总费用不超过12000元,求该校本次购买A种口罩最少有多少包?24. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)、若AC=6,DM=2,求△ACD的面积;(2)、求证:AC=BM+CM.23. 戴口罩可以有效降低感染新型冠状病毒的风险.某学校在本学期开学初为八年级学生购买A、B两种口罩,经过市场调查,每包A口罩比每包B口罩少10元,花费400元购买A口罩和花费600元购买B口罩的数量相等.(1)、求A、B两种口罩每包的价格各是多少元?(2)、若学校需购买两种口罩共500包,总费用不超过12000元,求该校本次购买A种口罩最少有多少包?24. 如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.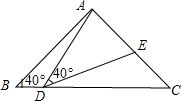 (1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.25. 如图1,已知点A(a,0),点B(0,b),且a、b满足+|4﹣b|=0.
(1)、当∠BDA=115°时,∠EDC=°,∠DEC=°;点D从B向C运动时,∠BDA逐渐变(填“大”或“小”);(2)、当DC等于多少时,△ABD≌△DCE,请说明理由;(3)、在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.25. 如图1,已知点A(a,0),点B(0,b),且a、b满足+|4﹣b|=0. (1)、求A、B两点的坐标;(2)、若点C是第一象限内一点,且∠OCB=45°,过点A作AD⊥OC于点F,求证:FA=FC;(3)、如图2,若点D的坐标为(0,1),过点A作AE⊥AD,且AE=AD,连接BE交x轴于点G,求G点的坐标.
(1)、求A、B两点的坐标;(2)、若点C是第一象限内一点,且∠OCB=45°,过点A作AD⊥OC于点F,求证:FA=FC;(3)、如图2,若点D的坐标为(0,1),过点A作AE⊥AD,且AE=AD,连接BE交x轴于点G,求G点的坐标.