浙江省宁波市2023-2024学年九年级上学期期末数学预考练习卷
试卷更新日期:2024-01-30 类型:期末考试
一、选择题(本大题共10小题,每小题4分,共40分)
-
1. 已知的半径为5,点P在内,则OP的长可能是( )A、4 B、5 C、5.5 D、62. 如图,在地面上的点A处测得树顶B的仰角为a , 米,则树高为( )
 A、米 B、米 C、米 D、 米3. 如图,已知 , , , 的长为( )
A、米 B、米 C、米 D、 米3. 如图,已知 , , , 的长为( ) A、2 B、4 C、3 D、54. 如图,点A,B,C都在⊙O上,若∠BAC=38°,则∠BOC的度数为( )
A、2 B、4 C、3 D、54. 如图,点A,B,C都在⊙O上,若∠BAC=38°,则∠BOC的度数为( )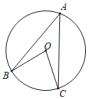 A、80° B、76° C、62° D、52°5. 关于二次函数 , 下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数的最大值是5 D、当时,y随x的增大而增大6. “石头、剪刀、布”是我国古老的民间游戏,游戏规定:石头胜剪刀,剪刀胜布,布胜石头,若两人的手势相同,不分胜负.在学校组织的“共情陪伴,健康同行”亲子运动会上,
A、80° B、76° C、62° D、52°5. 关于二次函数 , 下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数的最大值是5 D、当时,y随x的增大而增大6. “石头、剪刀、布”是我国古老的民间游戏,游戏规定:石头胜剪刀,剪刀胜布,布胜石头,若两人的手势相同,不分胜负.在学校组织的“共情陪伴,健康同行”亲子运动会上,爸爸和小亮用这种方式决定“打乒乓球”的发球权.从概率的角度思考这个游戏是否公平( )
 A、公平 B、对爸爸有利 C、对小亮有利 D、不能判断7. 如图,小明在A时测得某树的影长为 , B时又测得该树的影长为 , 若两次日照的光线互相垂直,则树的高度为( )
A、公平 B、对爸爸有利 C、对小亮有利 D、不能判断7. 如图,小明在A时测得某树的影长为 , B时又测得该树的影长为 , 若两次日照的光线互相垂直,则树的高度为( )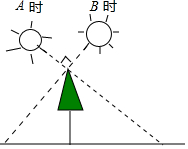 A、 B、 C、 D、8. 如图,在边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为( )
A、 B、 C、 D、8. 如图,在边长为1的小正方形构成的网格中,点A,B,C都在格点上,以AB为直径的圆经过点C,D,则tan∠ADC的值为( ) A、 B、 C、 D、9. 如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若米,则点到直线距离为( )
A、 B、 C、 D、9. 如图,在处测得点在北偏东方向上,在处测得点在北偏东方向上,若米,则点到直线距离为( )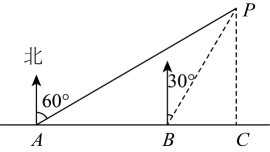 A、米 B、米 C、米 D、米10. 已知二次函数的图象如图所示,有下列结论:①;②;③;④其中 , 其中正确的结论有( )
A、米 B、米 C、米 D、米10. 已知二次函数的图象如图所示,有下列结论:①;②;③;④其中 , 其中正确的结论有( )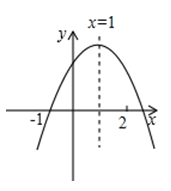 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题共6小题,每小题5分,共30分.不需写出解答过程,请将正确答案填写在横线上)
-
11. 连续投掷两枚质地均匀的硬币,两枚硬币恰好是一正一反的概率是
 12. 在中, , , 则13. 一辆汽车行驶的路程(单位:m)关于时间(单位:s)的函数解析式是 ,经过16s汽车行驶了m.14. 如图,已知△ABC中,点D在AB上,点E在AC上,DE∥BC.AD=2,DB=3,AE=4,则EC=;
12. 在中, , , 则13. 一辆汽车行驶的路程(单位:m)关于时间(单位:s)的函数解析式是 ,经过16s汽车行驶了m.14. 如图,已知△ABC中,点D在AB上,点E在AC上,DE∥BC.AD=2,DB=3,AE=4,则EC=; 15. 如图,正五边形的边长为 , 以为圆心,以为半径作弧 , 则阴影部分的面积为(结果保留).
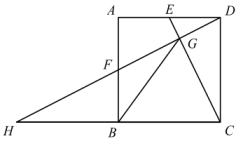
15. 如图,正五边形的边长为 , 以为圆心,以为半径作弧 , 则阴影部分的面积为(结果保留). 16. 如图,在正方形中,为的中点,为的中点,
16. 如图,在正方形中,为的中点,为的中点,的延长线与的延长线交于点 , 与相交于点 . 若 , 则的长为 .
三、解答题(本大题共8小题,共80分.解答时应写出文字说明、证明过程或演算步骤)
-
17.(1)、计算:.(2)、求二次函数的图象与x轴的交点坐标.18. 在一次宣传杭州亚运会的有奖竞猜活动中,获奖者从放有只有颜色不同的3个小球(1个黑球,1个白球,1个黄球)的不透明布袋中摸球,若摸到一个黑球奖励一个亚运会吉祥物“宸宸”,摸到一个白球奖励一个“琮琮”,摸到一个黄球奖励一个“莲莲”.一个获奖者先从布袋中任意摸出一球,不放回,再摸出一球,求得到一个“莲莲”和一个“琮琮”的概率.
 19. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)
19. 如图,在的正方形网格中,每个小正方形的顶点叫做格点,经过格点 , 仅用无刻度的直尺在给定网格中画图.(保留作图痕迹)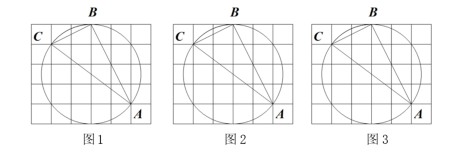 (1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.20. 一家商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售、增加盈利,该店采取降价措施,在每件盈利不少于24元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、求每件商品降价多少元时,该商店每天销售利润为1200元.(2)、求每件商品降价多少元时,该商店每天销售利润最大,最大利润是多少元?21. 如图1,是一款手机支架图片,由底座、支撑板和托板构成.如图2是其侧面结构示意图,量得托板长 , 支撑板长 , 底座长 , 托板AB连接在支撑板顶端点C处,且 , 托板可绕点C转动,支撑板可绕D点转动.如图2,若 .
(1)、在图1中,画出的中线.(2)、在图2中,标出圆心 , 并画出的角平分线.(3)、在图3中,画出的边上的高线.20. 一家商店销售某种商品,平均每天可售出20件,每件盈利40元,为了扩大销售、增加盈利,该店采取降价措施,在每件盈利不少于24元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、求每件商品降价多少元时,该商店每天销售利润为1200元.(2)、求每件商品降价多少元时,该商店每天销售利润最大,最大利润是多少元?21. 如图1,是一款手机支架图片,由底座、支撑板和托板构成.如图2是其侧面结构示意图,量得托板长 , 支撑板长 , 底座长 , 托板AB连接在支撑板顶端点C处,且 , 托板可绕点C转动,支撑板可绕D点转动.如图2,若 .(参考数值 , , )
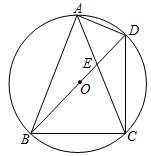
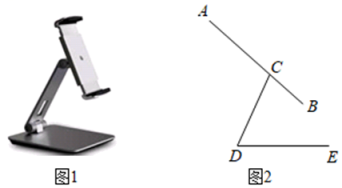 (1)、求点C到直线的距离(精确到0.1cm);(2)、求点A到直线的距离(精确到0.1cm).22. 如图,为半圆O的直径,C为半圆上一点,连接 , 点D为的中点,过D作 , 交的延长线于点E.
(1)、求点C到直线的距离(精确到0.1cm);(2)、求点A到直线的距离(精确到0.1cm).22. 如图,为半圆O的直径,C为半圆上一点,连接 , 点D为的中点,过D作 , 交的延长线于点E.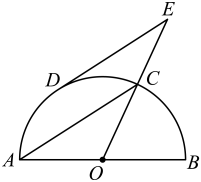 (1)、求证:是半圆O的切线.(2)、若 , , 求的长.
(1)、求证:是半圆O的切线.(2)、若 , , 求的长.