广东省惠州市博罗县2023-2024学年八年级上学期期末模拟数学试题

试卷更新日期：2024-01-30 类型：期末考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分）

1. 下面四个图形标志中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（　　）

A、a⁶÷a³＝a² B、（2a）³＝2a³ C、a³+a³＝a⁶ D、（a²）³＝a⁶

查看试题解析
3. 生物学家发现了一种病毒，其长度约为0.00000032mm，数据0.00000032用科学记数法表示正确的是（　　）

A、3.2×10⁷ B、3.2×10⁸ C、3.2×10^-7 D、3.2×10^-8

查看试题解析
4. 如图，人字梯中间一般会设计一“拉杆”，以增加使用梯子时的安全性，这样做蕴含的道理是（）

A、两点之间线段最短 B、三角形具有稳定性 C、经过两点有且只有一条直线 D、垂线段最短

查看试题解析
5. 代数式 $\frac{1}{y} ， \frac{3}{4} ， \frac{x + 1}{2} ， \frac{a + b}{π} ， c + \frac{4}{n}$ 中，分式的个数是（）

A、2个　　 B、3个　　 C、4个　　 D、5个

查看试题解析
6. 等腰三角形的两边长分别为4cm和8cm，则它的周长为（　　）

A、16cm B、17cm C、20cm D、16cm或20cm

查看试题解析
7. 若 $a^{m} = 4$ ， $a^{n} = 6$ ，则 $a^{m + n} =$ （）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $10$ D、 $24$

查看试题解析
8. A、B两地相距48 $k m$ ，一艘轮船从 $A$ 地顺流航行至B地，比从B地逆流航行至 $A$ 地少用 $2 h$ ，已知水流速度为 $5 k m / h$ ，求该轮船在静水中的航行速度是多少 $k m / h$ ？若设该轮船在静水中的速度为 $x k m / h$ ，则可列方程（）

A、 $\frac{48}{x - 5} - \frac{48}{x + 5} = 2$ B、 $\frac{48}{x + 5} - \frac{48}{x - 5} = 2$ C、 $\frac{x + 5}{48} - \frac{x - 5}{48} = 2$ D、 $\frac{x - 5}{48} + \frac{x + 5}{48} = 2$

查看试题解析
9. 如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点．若PA = 2，则PQ的长不可能是（）

A、4 B、3.5 C、2 D、1.5

查看试题解析
10. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P₁ ， P₂ ， P₃ ， P₄四个点中找出符合条件的点P，则点P有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本题共5小题，每小题3分，共15分）

11. 使分式 $\frac{x - 1}{x + 3}$ 有意义的 $x$ 满足．

查看试题解析
12. 已知一个多边形的内角和是 $720 °$ ，则这个多边形有条边．

查看试题解析
13. 若x²+ax+4是完全平方式，则a= ．

查看试题解析
14. 如图所示的两个三角形全等，则∠1的度数是 .

查看试题解析
15. 如图，在△ABC中， $∠ A C B = 90 °$ ， $∠ A = 60 °$ ，分别以点A和点B为圆心以相同的长（大于 $\frac{1}{2} A B$ ）为半径作弧，两弧相交于M和N点，作直线 $M N$ 交 $A B$ 于点D，交 $B C$ 于点E，若 $B C = 4$ ，则 $B E$ 等于．

查看试题解析

三、解答题（一）（本题共3小题，16题10分，17题、18题7分，共24分）

16. 计算：

(1)、 ${(- 1)}^{2} + {(\frac{1}{2})}^{- 1} - 5 \div {(2004 - π)}^{0}$

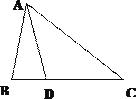
(2)、计算： ${(x - 3)}^{2} - (x - 2) (x + 2)$

查看试题解析
17. 甲、乙二人做某种机械零件．已知甲每小时比乙多做 $6$ 个，甲做 $90$ 个所用的时间与乙做 $60$ 个所用的时间相等．求甲、乙每小时各做零件多少个．

查看试题解析
18.
如图，在△ABC中，AB=AD=DC，∠BAD=26°，求∠B和∠C的度数.

查看试题解析

四、解答题（二）（本大题共3小题，每小题9分，共27分）

19. 先化简 $(x - \frac{2 x - 1}{x}) \div \frac{x^{2} - x}{x^{2}}$ ，再从﹣1，0，1中选择一个合适的数代入求值．

查看试题解析
20. 如图，在Rt△ABC中，AC=BC，∠ACB=90°，BF平分∠ABC交AC于点F，AE⊥BF于点E，AE，BC的延长线交于点M.

(1)、求证：AB=BM；

(2)、求证：BF=2AE.

查看试题解析
21. 如图，△ABC三个顶点的坐标分别为 $A (- 4 ， - 2)$ ， $B (- 1 ， - 1)$ ， $C (- 1 ， - 4)$ ．

(1)、画出△ABC关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；△ABC内有一点 $P (a ， b)$ ，则点P关于y轴的对称点 $P_{1}$ 的坐标为（ ▲ ， ▲ ）

(2)、求△ABC的面积：

(3)、在x轴上作出一点P，使 $P A + P B$ 的值最小．（保留作图痕迹）

查看试题解析

五、解答题（三）（本题共2小题，每小题12分，共24分）

22. 数与形是数学研究的两大部分，它们间的联系称为数形结合，数形结合大致分为两种情形，或者借助图形的直观来阐明数之间的关系，或者借助数的精确性来阐明图形的属性，即“以形助数”或“以数解形”，整式乘法中也利用图形面积来论证数量关系．现用砖块相同的面（如材料图，长为a，宽为b的小长方形）拼出以下图形，延长部分边框，则把这些拼图置于如图所示的正方形或大长方形内，请解答下列问题．

(1)、求图1中空白部分的面积 $S_{1}$ （用含 $a b$ 的代数式表示）．

(2)、图1，图2中空白部分面积 $S_{1}$ 、 $S_{2}$ 分别为19、68，求 $a b$ 值．

(3)、图3中空白面积为S，根据图形中的数量关系，将下列式子因式分解：
① $S_{3} + 7 a b =$ ；
② $S_{3} - a^{2} + 5 a b =$ ．

查看试题解析
23. 阅读下面材料：
小明遇到这样一个问题：
如图9-①，在△ABC中，AD平分∠BAC，∠ABC=2∠C，求证：AC=AB+BD；
小明通过思考发现，可以通过“截长、补短”两种方法解决问题：
方法一：如图9-②，在AC上截取AE，使得AE=AB，连接DE，可以得到全等三角形，进而解决问题；
方法二：如图9-③，延长AB到点E，使得BE=BD，连接DE，可以得到等腰三角形，进而解决问题.

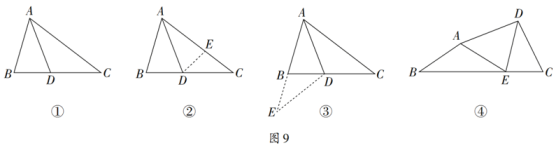(1)、根据以上材料，任选一种方法证明：AC=AB+BD；

(2)、如图9-④，四边形ABCD中，E是BC上一点，EA=ED，
∠C=2∠B，∠DAE+∠B=90°，探究DC，CE，BE之间的数量关系，并证明.

查看试题解析