广东省广州重点学校2023-2024学年高三上学期期末考试数学试题

试卷更新日期：2024-01-30 类型：期末考试

进入出卷网下载

一、单选题:本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 已知集合 $A = {x | x > 1}$ ， $B = {x | x^{2} - 2 x - 3 > 0}$ ，则 $A \cup B =$ （）

A、 $(3 ， + \infty)$ B、（1，3） C、 $(- \infty ， - 1) \cup (1 ， + \infty)$ D、 $(- \infty ， - 1) \cup (3 ， + \infty)$

查看试题解析
2. 已知 $a > b$ ，则下列不等式中成立的是（）

A、 $a b > b^{2}$ B、 $a^{2} > b^{2}$ C、 $\frac{1}{a} < \frac{1}{b}$ D、 $2^{a} > 2^{b}$

查看试题解析
3. 复数z满足 ${(2 - i)}^{2} z = - i$ ，则 $\bar{z}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 若 $P (A B) = \frac{1}{9} ， P (\bar{A}) = \frac{2}{3} ， P (B) = \frac{1}{3}$ ，则事件 $A$ 与 $B$ 的关系是（）

A、事件 $A$ 与 $B$ 互斥 B、事件 $A$ 与 $B$ 对立 C、事件 $A$ 与 $B$ 相互独立 D、事件 $A$ 与 $B$ 既互斥又相互独立

查看试题解析
5. 《宋人扑枣图轴》是作于宋朝的中国古画，现收藏于中国台北故宫博物院．有甲、乙，丙，丁想根据该图编排一个舞蹈，图中的小孩扑枣有爬、扶、捡、顶四个的动作，每人模仿一个动作，若他们采用抽签的方式来决定谁模仿哪个动作，则甲只能模仿“爬”或“扶”且乙只能模仿“扶”或“捡”的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6. 在 $(x + 1) {(x - 1)}^{5}$ 展开式中 $x^{3}$ 的系数为（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
7. 已知 $a ， b \in R^{+}$ ，且 $a + 2 b = 3 a b$ ，则 $2 a + b$ 的最小值为（）

A、3 B、4 C、6 D、9

查看试题解析
8. 设随机变量 $X ~ B (n ， p)$ ，若二项式 $(x + p)^{n} = a_{0} + \frac{1}{2} x + \frac{3}{2} x^{2} + ⋯ + a_{n} x^{n}$ ，则（）

A、 $E (x) = 3$ ， $D (x) = 2$ B、 $E (x) = 4$ ， $D (x) = 2$ C、 $E (x) = 2$ ， $D (x) = 1$ D、 $E (x) = 3$ ， $D (x) = 1$

查看试题解析

二、多选题:本题共4小题，每小题5分，共20分. 完全正确得5分，漏选得2分，错选或不选不得分.

9. 下列命题正确的是 (　　)

A、“ $a > 1$ ”是“ $\frac{1}{a} < 1$ ”的充分不必要条件 B、命题“若 $x < 1 ，则 x^{2} < 1$ ”的否定是“存在 $x < 1 ，则 x^{2} \geq 1$ ” C、设x，y∈R，则“x≥2且y≥2”是“ $x^{2} + y^{2} \geq 4$ ”的必要而不充分条件 D、设a，b∈R，则“a≠0”是“ab≠0”的必要而不充分条件

查看试题解析
10. 在 ${(x - \frac{2}{x})}^{5}$ 的展开式中，下列说法正确的是（）

A、不存在常数项 B、所有二项式系数的和为32 C、第3项和第4项二项式系数最大 D、所有项的系数和为1

查看试题解析
11. 有3台车床加工同一型号的零件.第1台加工的次品率为6% ，第2，3台加工的次品率均为5%，加工出来的零件混放在一起.已知第1，2，3台车床的零件数分别占总数的25%，30%，45%，则下列选项正确的有（）

A、任取一个零件是第1台生产出来的次品概率为0. 06 B、任取一个零件是次品的概率为0. 0525 C、如果取到的零件是次品，且是第2台车床加工的概率为 $\frac{2}{7}$ D、如果取到的零件是次品，且是第3台车床加工的概率为 $\frac{2}{7}$

查看试题解析
12. 下列说法正确的是（）

A、某射击运动员在一次训练中10次射击成绩（单位：环）如下：6，5，7，9，6，8，9，9，7，5，这组数据的第70百分位数为8 B、对于随机事件A与B ，若 $P (\bar{B}) = 0.3 ， P (B | A) = 0.7$ ，则事件A与B独立 C、若二项式 $(\frac{1}{2} - x)^{n}$ 的展开式中所有项的系数和为 $- \frac{1}{128}$ ，则展开式共有7项 D、设随机变量 $ξ$ 服从正态分布 $N (0 ， 1)$ ，若 $P (ξ > 1) = p$ ，则 $P (- 1 < ξ < 0) = \frac{1}{2} - p$

查看试题解析

三、填空题:本题共4小题，每小题5分，共20分.

13. 复数 $z = \frac{2}{- 1 + i}$ 的虚部是

查看试题解析
14. 已知随机变量 $ξ$ 服从正态分布 $N (4 ， σ^{2})$ ，且 $P (ξ > 6) = 0.2$ ，则 $P (2 < ξ < 4) =$ .

查看试题解析
15. 现有 $A ， B ， C ， D ， E$ 五人排成一列，其中 $A$ 与 $B$ 相邻， $C$ 不排在两边，则共有种不同的排法（用具体数字作答）．

查看试题解析
16. 对 $\forall x \in R$ ，不等式 $(a - 2) x^{2} + 2 (a - 2) x - 4 < 0$ 恒成立，则a的取值范围是

查看试题解析

四、解答题：本题共6小题，共70分.17题10分，18^22每题12分.解答应写出文字说明、证明过程或演算步骤.

17. 设 $p ： \frac{x - 2}{x - 4} \leq 0$ ， $q$ ：实数 $x$ 满足 $x^{2} - 2 a x - 3 a^{2} < 0 (a > 0)$ .

(1)、若 $a = 1$ ，且 $p ， q$ 都为真命题，求x的取值范围；

(2)、若 $p$ 是 $q$ 的充分不必要条件，求实数 $a$ 的取值范围.

查看试题解析
18. 某学校共有1000名学生参加知识竞赛，其中男生400人，为了解该校学生在知识竞赛中的情况，采取分层抽样随机抽取了100名学生进行调查，分数分布在 $450 \sim 950$ 分之间，根据调查的结果绘制的学生分数频率分布直方图如图所示：
将分数不低于750分的学生称为“高分选手”．

(1)、求 $a$ 的值，并估计该校学生分数的平均数、中位数和众数（同一组中的数据用该组区间的中点值作代表）；

(2)、现采用分层抽样的方式从分数落在 $[550 ， 650)$ ， $[750 ， 850)$ 内的两组学生中抽取10人，再从这10人中随机抽取3人，记被抽取的3名学生中属于“高分选手”的学生人数为随机变量 $X$ ，求 $X$ 的分布列及数学期望；

查看试题解析
19. 已知关于x的不等式ax²﹣x+1﹣a＜0．

(1)、当a＝2时，解关于x的不等式；

(2)、当a＞0时，解关于x的不等式．

查看试题解析
20. 多巴胺是一种神经传导物质，能够传递兴奋及开心的信息.近期很火的多巴胺穿搭是指通过服装搭配来营造愉悦感的着装风格，通过色彩艳丽的时装调动正面的情绪，是一种“积极化的联想”.小李同学紧跟潮流，她选择搭配的颜色规则如下：从红色和蓝色两种颜色中选择，用“抽小球”的方式决定衣物颜色，现有一个箱子，里面装有质地、大小一样的4个红球和2个白球，从中任取4个小球，若取出的红球比白球多，则当天穿红色，否则穿蓝色.每种颜色的衣物包括连衣裙和套装，若小李同学选择了红色，再选连衣裙的可能性为0.6，而选择了蓝色后，再选连衣裙的可能性为0.5.

(1)、写出小李同学抽到红球个数的分布列及期望；

(2)、求小李同学当天穿连衣裙的概率.

查看试题解析
21. 从2013年开始.的9年来，某地区第 $x$ 年的第三产业生产总值 $y$ （单位：百万元）统计图如下图所示.根据该图提供的信息解决下列问题.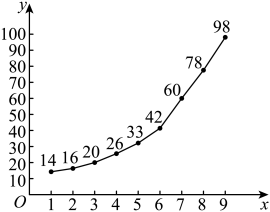

(1)、在所统计的9个生产总值中任选2个，记其中不低于平均值的个数为 $X$ ，求 $X$ 的分布列和数学期望 $E (X)$ ；

(2)、由统计图可看出，从第6年开始，该地区第三产业生产总值呈直线上升趋势，试从第6年开始用线性回归模型预测该地区第11年的第三产业生产总值.
（附：对于一组数据 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ， …， $(x_{n} ， y_{n})$ ，其回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 的斜率和截距的最小二乘法估计分别为： $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ .

查看试题解析
22. 为了迎接2022年世界杯足球赛，某足球俱乐部在对球员的使用上一般都进行一些数据分析，在上一年的赛季中，A球员对球队的贡献度数据统计如下：

球队胜
球队负
总计
$A$ 上场
22
$r$

$A$ 未上场
$s$
12
20
总计

50

(1)、求 $r ， s$ 的值，据此能否有 $99 %$ 的把握认为球队胜利与 $A$ 球员有关；

(2)、根据以往的数据统计， $B$ 球员能够胜任前锋､中锋､后卫以及守门员四个位置，且出场率分别为： $0.2 ， 0.3 ， 0.2 ， 0.3$ ，当出任前锋､中锋､后卫以及守门员时，球队赢球的概率依次为： $0.2 ， 0.2 ， 0.4 ， 0.3$ ，则：
①当他参加比赛时，求球队某场比赛赢球的概率；
②当他参加比赛时，在球队赢了某场比赛的条件下，求 $B$ 球员担当守门员的概率；
③在2022年的4场联赛中，用X表示“球队赢了比赛的条件下 $B$ 球员担当守门员”的比赛场次数，求 $X$ 的分布列及期望．
附表及公式：
$P (χ^{2} ≥ k)$
$0.15$
$0.10$
$0.05$
$0.010$
$0.005$
$0.001$
$k$
$2.072$
$2.706$
$3.841$
$6.635$
$7.879$
$10.828$
$\begin{matrix} χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)} \end{matrix}$ ．

查看试题解析

	球队胜	球队负	总计
$A$ 上场	22	$r$
$A$ 未上场	$s$	12	20
总计			50

$P (χ^{2} ≥ k)$	$0.15$	$0.10$	$0.05$	$0.010$	$0.005$	$0.001$
$k$	$2.072$	$2.706$	$3.841$	$6.635$	$7.879$	$10.828$