广东省深圳市2023-2024学年重点中学高一(上)期末数学试卷
试卷更新日期:2024-01-30 类型:期末考试
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 函数的定义域为( )A、 B、 C、 D、2. 若命题“ , ”是假命题,则实数的取值范围为( )A、 B、 C、 D、3. “ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 已知函数 , 且的图象恒过点 , 若角的终边经过点 , 则( )A、 B、 C、 D、5. 下列是奇函数,且在区间上单调递增的是( )A、 B、 C、 D、6. 已知实数m、n满足2m+n=2,其中mn>0,则 的最小值为( )A、4 B、6 C、8 D、127. 将函数图象上各点的横坐标伸长到原来的2倍,再向左平移个单位,纵坐标不变,所得函数图象的一条对称轴的方程是( )A、 B、 C、 D、8. 根据国家有关规定:驾驶人血液中的酒精含量大于或等于毫克毫升属于酒驾假设某驾驶员一天晚上点钟喝了一定量的酒后,其血液中酒精含量上升到毫克毫升如果在停止喝酒后,他血液中酒精含量以每小时的速度减少,则他次日上午最早点结果取整数开车才不构成酒驾参考数据: , ( )A、 B、 C、 D、
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
-
9. 下列是函数图象的是( )A、
 B、
B、
C、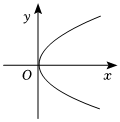 D、
D、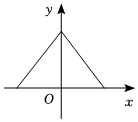 10. 已知函数 , 下列说法正确的是( )A、的定义域是 B、的图象关于原点对称
10. 已知函数 , 下列说法正确的是( )A、的定义域是 B、的图象关于原点对称
C、 D、当时,的最小值为11. 已知的定义域是 , 既是奇函数又是减函数.若 , , 且 , 则( )A、 B、 C、 D、12. 若函数的图象是连续的,且函数的唯一零点同在区间 , , , 内,则与符号不同的是( )A、 B、 C、 D、三、填空题:本题共4小题,每小题5分,共20分。
-
13. 已知 , 计算: .14. 若函数 , 则 .15. 若、是关于的方程的两个根,则.16. 设当时,函数 , 取得最大值,则 .
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
-
17. 设 , 已知集合 , .(1)、当时,求;(2)、若 , 且 , 求实数的取值范围.18. 已知二次函数且 , .
(1)、若函数的最小值为 , 求的解析式,并写出单调区间;(2)、在的条件下,在区间上恒成立,试求的取值范围.19. 已知函数 , .
(1)、求函数的最小正周期与单调增区间;(2)、求函数在上的最大值与最小值.