浙江省温州名校2023-2024学年高一上学期数学12月月考试卷

试卷更新日期：2024-01-30 类型：月考试卷

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 命题“ $\forall x \in R ， \sin x + 1 \geq 0$ ”的否定是（）

A、 $\exists x_{0} \in R ， \sin x_{0} + 1 < 0$ B、 $\forall x \in R ， \sin x + 1 < 0$ C、 $\exists x_{0} \in R ， \sin x_{0} + 1 \geq 0$ D、 $\forall x \in R ， \sin x + 1 \leq 0$

查看试题解析
2. 若 $M = {x | l o g_{2} (x - 1) < 1}$ ， $N = {x | x^{2} - (a + 1) x + a < 0}$ ，则“ $a \leq 2$ ”是“ $N \subseteq M$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知扇形的圆心角为2弧度，且圆心角所对的弦长为4，则该扇形的面积为（）

A、 $\frac{4}{s i n^{2} 1}$ B、 $\frac{4}{c o s^{2} 1}$ C、 $4 s i n^{2} 1$ D、 $4 c o s^{2} 1$

查看试题解析
4. 已知函数y＝f（x）的部分图象如图所示，则函数f（x）的解析式最可能是（）

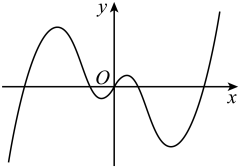A、y＝xcosx B、y＝sinx－x² C、 $y = \frac{1 - c o s x}{2^{x}}$ D、y＝sinx＋x

查看试题解析
5. $a = s i n 1$ ， $b = l g s i n 1$ ， $c = 1 0^{s i n 1}$ ，则（）

A、 $a < b < c$ B、 $b < a < c$ C、 $b < c < a$ D、 $c < b < a$

查看试题解析
6. 已知函数 $f (x) = \frac{2^{x} s i n λ x}{2^{λ x} + 1}$ 是奇函数，则实数 $λ =$ （）

A、 $- 2$ B、 $- 1$ C、1 D、2

查看试题解析
7. 若函数 $f (x) = {\begin{array}{l} l o g_{2} x + 2 x ， x > 0 \\ s i n (ω x + \frac{π}{3}) ， - π \leq x \leq 0 \end{array}$ 有4个零点，则正数 $ω$ 的取值范围是（）

A、 $[\frac{4}{3} ， \frac{7}{3})$ B、 $[\frac{7}{3} ， \frac{10}{3})$ C、 $(\frac{4}{3} ， \frac{7}{3}]$ D、 $(\frac{7}{3} ， \frac{10}{3}]$

查看试题解析
8. 若 $x > 0$ ， $y > 1$ ，则 $\frac{4 y}{x} + \frac{x^{3}}{y - 1}$ 的最小值为（）

A、4 B、 $4 \sqrt{2}$ C、8 D、 $8 \sqrt{2}$

查看试题解析

二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．

9. 下列函数中，在区间 $(1 ， 2)$ 上为增函数的是（）

A、 $y = 2^{x + 1}$ B、 $y = l o g_{2} (x - 1)$ C、 $y = x | x - 2 |$ D、 $y = t a n x$

查看试题解析
10. 已知函数 $f (x) = A c o s (ω x + φ)$ （ $A > 0$ ， $ω > 0$ ， $0 < φ < π$ ）在 $x = \frac{5 π}{12}$ 处取得最小值 $- 2$ ，与此最小值点相邻的 $f (x)$ 的一个零点为 $\frac{π}{6}$ ，则（）

A、 $w = 2$ B、 $φ = \frac{2 π}{3}$ C、 $y = f (x - \frac{π}{3})$ 是奇函数 D、 $f (x)$ 在 $(- \frac{π}{6} ， \frac{π}{3})$ 上单调递减

查看试题解析
11. 设 $a$ ， $b$ 为正数，且 $a - 5 b - 4 a b = 1$ ，则（）

A、 $a > 1$ B、 $b > \frac{1}{4}$ C、 $\frac{b}{a} \leq \frac{1}{25}$ D、 $a + 3 \geq 49 b$

查看试题解析
12. 记区间M＝[a ， b]，集合N＝{y|y＝ $\frac{k | x |}{| x | + 1}$ ， x∈M}，若满足M＝N成立的实数对（a ， b）有且只有1个，则实数k可以取（）

A、﹣2 B、 $\frac{1}{2}$ C、1 D、3

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分．

13. 已知 $f (x) = {\begin{array}{l} x^{2} + 1 ， x \leq 1 \\ s i n x ， x > 1 \end{array}$ ，则 $f (f (\frac{25 π}{6})) =$ ．

查看试题解析
14. 已知函数 $f (x) = l o g_{a} (x + b)$ 的图象不经过第二、四象限，请写出满足条件的一组 $(a ， b)$ 的值.

查看试题解析
15. 已知 $s i n (θ + \frac{π}{3}) = \frac{4}{5}$ ， $- \frac{π}{3} < θ < \frac{π}{6}$ ，则 $t a n (2 θ + \frac{π}{6}) =$ ．

查看试题解析
16. 理论上，一张纸经过一定次数对折之后厚度能超过地月距离，但实际上，因为纸张本身有厚度，我们并不能将纸张无限次对折，当我们的厚度超过纸张的长边时，便不能继续对折了.一张长边为 $w$ ，厚度为 $x$ 的矩形纸张沿两个方向不断对折，则经过两次对折，长边变为 $\frac{1}{2} w$ ，厚度变为 $4 x$ .在理想情况下，对折次数 $n$ 有下列关系： $n \leq 2 l o g_{8} \frac{w}{x}$ ，根据以上信息，一张长为30 $c m$ ，厚度为0.05 $m m$ 的纸张最多能对折的次数为.

查看试题解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 设集合 $A = {x | l o g_{\frac{1}{2}} (2 x + 4) > l o g_{\frac{1}{2}} (x + 5)}$ ， $B = {x | x^{2} - m x + m = 0}$ ， $m \in R$ ．

(1)、若 $m = - 2$ ，求 $A \cap B$ ；

(2)、若 $A \cup B = A$ ，求实数 $m$ 的取值范围．

查看试题解析
18. 已知 $f (x) = 2 s i n x c o s (x + φ)$ （ $0 \leq φ \leq \frac{π}{2}$ ）．

(1)、若 $f (x)$ 为偶函数，求 $φ$ 的值；

(2)、若 $f (x)$ 的最小值为 $- \frac{3}{2}$ ，求 $f (x)$ 的对称中心．

查看试题解析
19. 设函数 $f (x) = \frac{a x}{b + x^{2}} (a \neq 0 ， x > 0)$ ，满足：① $f (1) = \frac{1}{2}$ ；②对任意 $x > 0$ ， $f (x) = f (\frac{1}{x})$ 恒成立．

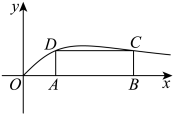(1)、求函数 $f (x)$ 的解析式．

(2)、设矩形 $A B C D$ 的一边 $A B$ 在 $x$ 轴上，顶点 $C$ ， $D$ 在函数 $f (x)$ 的图象上．设矩形 $A B C D$ 的面积为 $S$ ，求证： $0 < S < 1$ ．

查看试题解析
20. 已知函数 $f (x) = 3^{x} + a \cdot 3^{- x}$ 为偶函数.

(1)、求实数 $a$ 的值；

(2)、若关于 $x$ 的不等式 $f (2 x) - m f (x) \geq 0$ 恒成立，求实数 $m$ 的取值范围；

(3)、设函数 $g (x) = f (x) + x - 3^{- x} - 3$ 的零点为 $x_{0}$ ，求证： $\frac{5}{2} < f (x_{0}) < \frac{29}{10}$ .

查看试题解析
21. 在月亮和太阳的引力作用下，海水水面发生的周期性涨落现象叫做潮汐．一般早潮叫潮，晚潮叫汐．受潮汐影响，港口的水深也会相应发生变化．下图记录了某港口某一天整点时刻的水深y（单位：米）与时间x（单位：时）的大致关系：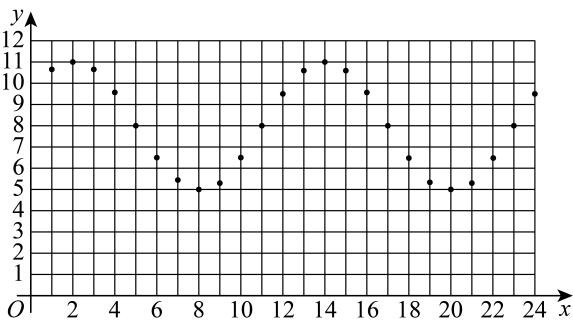
假设4月份的每一天水深与时间的关系都符合上图所示．

(1)、请运用函数模型 $y = A s i n (ω x + φ) + h (A > 0 ， ω > 0 ， - \frac{π}{2} < φ < \frac{π}{2} ， h \in R)$ ，根据以上数据写出水深y与时间x的函数的近似表达式；

(2)、根据该港口的安全条例，要求船底与水底的距离必须不小于3.5米，否则该船必须立即离港．一艘船满载货物，吃水（即船底到水面的距离）6米，计划明天进港卸货．
①求该船可以进港的时间段；
②该船今天会到达港口附近，明天0点可以及时进港并立即开始卸货，已知卸货时吃水深度以每小时0.3米的速度匀速减少，卸完货后空船吃水3米．请设计一个卸货方案，在保证严格遵守该港口安全条例的前提下，使该船明天尽早完成卸货（不计停靠码头和驶离码头所需时间）．

查看试题解析
22. 设函数 $f (x) = a (c o s 2 x + c o s x + 1) - c o s x - 1$ ， $g (x) = - 2 a s i n 2 x + (1 - a) s i n x$ ，其中 $a > 0$ ．

(1)、当 $a = 2$ 时，求函数 $f (x)$ 的值域；

(2)、记 $| f (x) |$ 的最大值为M ，
①求M；
②求证： $| g (x) | \leq 2 M$ ．

查看试题解析