2023-2024学年沪科版初中数学九年级下册 24.7.2 圆锥的侧面展开图及计算 同步分层训练培优卷
试卷更新日期：2024-01-29 类型：同步测试
一、选择题
-
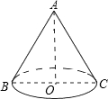
1. 如图，AB是圆锥的母线，BC为底面直径，已知BC=6cm，圆锥的侧面积为 ， 则的值为（ ）
A、 B、 C、 D、2. 用一个圆心角为 ， 半径为8的扇形作一个圆锥的侧面，则这个圆锥的底面直径是（ ）A、6 B、5 C、4 D、33. 如图，已知圆锥侧面展开图的扇形面积为 ， 扇形的弧长为 ， 则圆锥的高是（ ）
A、 B、 C、 D、4. 如图，小红要制作一个母线长为 ， 底面圆半径是的圆锥形小漏斗，若不计损耗，则所需纸板的面积是（ ）
A、 B、 C、 D、5. 如图，从一张腰长为90cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD，用此剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的底面圆的半径为（ ）cm．
A、15 B、30 C、45 D、30π6. 如图，圆锥的母线长为5cm ， 高线长为4cm ， 则圆锥的表面积是（ ）
A、9πcm2 B、24πcm2 C、30πcm2 D、39πcm27. 将一个直角三角形以一条直角边所在的直线为轴旋转一周，得到一个圆锥，若这个直角三角形斜边的长为 ， 圆锥的侧面积为 ， 则该圆锥的高为（ ）A、 B、 C、 D、8. 正如我们小学学过的圆锥体积公式V= πr2h（π表示圆周率，r表示圆锥的底面半径，h表示圆锥的高）一样，许多几何量的计算都要用到π．祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家，创造了当时世界上的最高水平，差不多过了1000年，才有人把π计算得更精确．在辉煌成就的背后，我们来看看祖冲之付出了多少．现在的研究表明，仅仅就计算来讲，他至少要对9位数字反复进行130次以上的各种运算，包括开方在内．即使今天我们用纸笔来算，也绝不是一件轻松的事情，何况那时候没有现在的纸笔，数学计算不是用现在的阿拉伯数字，而是用算筹（小竹棍或小竹片）进行的，这需要怎样的细心和毅力啊！他这种严谨治学的态度，不怕复杂计算的毅力，值得我们学习．下面我们就来通过计算解决问题：已知圆锥的侧面展开图是个半圆，若该圆锥的体积等于9 π，则这个圆锥的高等于（ ）
A、 B、 C、 D、二、填空题
-
9. 工人师傅用一张半径为24 cm，圆心角为150°的扇形铁皮做成一个圆锥的侧面（如图），则这个圆锥的高线长为cm.
10. 已知圆锥的母线长为 ， 底面半径为 ， 则它的侧面展开扇形的面积为 ．11. 如图，正六边形ABCDEF的边长为6，以顶点A为圆心，AB的长为半径画弧，则由图中阴影部分的扇形围成的圆锥的高为 ．
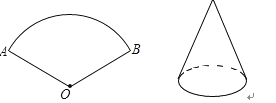
12.如图，将弧长为6π，圆心角为120°的圆形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（粘连部分忽略不计）则圆锥形纸帽的高是 ．
三、解答题
-
13. 如图，已知扇形 的圆心角为120º，半径为6cm.
(1)、请用尺规作出扇形的对称轴；(不写做法，保留作图痕迹)(2)、求扇形 的面积；(3)、若将此扇形围成一个圆锥的侧面(不计接缝)，求圆锥的底面圆面积.14. 如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
(1)、请在图中确定该圆弧所在圆心D点的位置 ， D点坐标为；(2)、连接AD、CD，求⊙D的半径及扇形DAC的圆心角度数；(3)、若扇形DAC是某一个圆锥的侧面展开图，求该圆锥的底面半径．四、综合题
-
15. 如图1，等腰三角形中，当顶角的大小确定时，它的对边（即底边）与邻边（即腰或）的比值也就确定了，我们把这个比值记作 ， 即 ，当时，如 ．
(1)、_ ， _ ， 的取值范围是_；(2)、如图2，圆锥的母线长为18，底面直径 ， 一只蚂蚁从点P沿着圆锥的侧面爬行到点Q，求蚂蚁爬行的最短路径长．（精确到0.1，参考数据： ， ）16. 综合与实践问题情境：如图1，将一个底面半径为r的圆锥侧面展开，可得到一个半径为l，圆心角为的扇形.工人在制作圆锥形物品时，通常要先确定扇形圆心角度数，再度量裁剪材料.
(1)、探索尝试：图1中，圆锥底面周长与其侧面展开图的弧长；（填“相等”或“不相等”）若 ， ， 则n=.(2)、解决问题：为操作简便，工人希望能简洁求n的值，请用含r，l的式子表示n；(3)、拓展延伸：图2是一种纸质圆锥形生日帽， ， ， C是中点，现要从点A到点C再到点A之间拉一装饰彩带，求彩带长度的最小值.