2023-2024学年沪科版初中数学九年级下册 24.7.1 弧长与扇形面积同步分层训练培优卷

试卷更新日期：2024-01-29 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2 $\sqrt{3}$ ，则阴影部分图形的面积为（）

A、4π B、2π C、π D、 $\frac{2 π}{3}$

查看试题解析
2. 如图所示，有一边长为6 cm的等边三角形ABC木块，点P是CA的延长线上的点，AP为15 cm，其中 $\overset{⏜}{P D}$ ， $\overset{⏜}{D F}$ ， $\overset{⏜}{F E}$ 的圆心依次为A，B，C，则曲线PDFE的长是（）

A、18π cm B、15π cm C、20π cm D、21π cm

查看试题解析
3. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，D是 $\overset{⌢}{A C}$ 的中点.若 $∠ A B D = 36 °$ ， $⊙ O$ 的半径为5，则 $\overset{⌢}{A C}$ 的长度为（）

A、 $2 π$ B、 $4 π$ C、 $6 π$ D、 $8 π$

查看试题解析
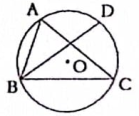4. 如图，扇形纸扇完全打开后，外侧两竹条AB，AC的夹角为120°，AB的长为30cm，贴纸部分BD的长为20cm，则贴纸部分的面积是（）

A、100πcm² B、 $\frac{400}{3}$ πcm² C、 $\frac{800}{3}$ πcm² D、800πcm²

查看试题解析
5. 已知点A ， B ， C在⊙O上，∠ABC＝30°，把劣弧 $\hat{B C}$ 沿着直线CB折叠交弦AB于点D ．若BD＝9，AD＝6，则 $\hat{A C}$ 的长为（）

A、 $2 \sqrt{3} π$ B、3π C、 $\frac{\sqrt{57}}{3} π$ D、 $\frac{5}{3} π$

查看试题解析
6. 如图，在矩形 $A B C D$ 中， $A B = 1 ， B C = \sqrt{3} ， P$ 是 $A D$ 边上的一个动点，连结 $B P$ ，点 $C$ 关于直线 $B P$ 的对称点为 $C_{1}$ ，当 $P$ 运动时， $C_{1}$ 也随之运动．若 $P$ 从 $A$ 运动到 $D$ ，则点 $C_{1}$ 经过的路径长是（）

A、 $\frac{2 \sqrt{3}}{3} π$ B、 $\frac{5 \sqrt{3}}{6} π$ C、 $\frac{4 π}{3}$ D、 $\frac{5 π}{3}$

查看试题解析
7. 已知点A，B，C在⊙O上，∠ABC=30°，把劣弧 $\overset{⌢}{B C}$ 沿着直线CB折叠交弦AB于点D．若BD=9，AD=6，则 $\overset{⌢}{A C}$ 的长为（）

A、 $2 \sqrt{3}$ π B、3π C、 $\frac{\sqrt{57}}{3}$ π D、 $\frac{5}{3}$ π

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ，半径为6的 $⊙ O$ 与 $A B$ 相切于点 $A$ ，与 $B C$ 交于点 $D$ ，连接 $O C$ ， $O D$ ， $A D$ ，有下列结论：① $C A$ 平分 $∠ O C D$ ；② $∠ A D B = ∠ A D O$ ；③若 $∠ A C B = 20 °$ ，扇形 $O A D$ 的面积为 $\frac{2}{3} π$ ；④若 $∠ A C B = 30 °$ ，则 $A C ⊥ O D$ ．其中正确的是（）

A、①③ B、②④ C、②③④ D、①②④

查看试题解析

二、填空题

9. 一个扇形的半径是 $3 c m$ ，圆心角是 $60 °$ ，则此扇形的面积是 $c m^{2}$ ．

查看试题解析
10. 如图，半圆的直径AB=4，C，D是半圆的三等分点，则弦 $A C$ ， $A D$ 与弧 $C D$ 围成的阴影部分的面积是．

查看试题解析
11. 如图，折扇的骨柄长为30cm，扇面宽度为18cm，折扇张开的角度为120°，则扇面外端 $\overset{⌢}{A B}$ 的长为cm，折扇扇面的面积为 ${cm}^{2}$ .（结果保留 $π$ ）

查看试题解析
12. 如图，在平面直角坐标系中，点 $P$ 的坐标是 $(8 ， 10)$ ， $⊙ P$ 与 $x$ 轴相切，点 $A$ ， $B$ 在 $⊙ P$ 上，它们的横坐标分别是0，18，若 $⊙ P$ 沿着 $x$ 轴作无滑动的滚动，当点 $B$ 第一次落在 $x$ 轴上时，此时点 $A$ 的坐标是．

查看试题解析
13. 量角器和三角板是我们平常数学学习中常用的工具．有一天，爱思考的小聪拿着两块工具拼成了如图1的样子，计划让三角板的直角顶点始终在量角器的半圆弧上运动，紧接着小聪根据自己的想法画出了示意图(如图2)。已知点C是量角器半圆弧的中点，点P为三角板的直角顶点，两直角边PE、PF分别过点A、B．连结CP，过点O作OM⊥CP交CP于点M，交AP于点N若AB=8，则NB的最小值为；若点Q为 $\overset{⌢}{B C}$ 的中点，则点P从点Q运动到点B时，N点的运动路径长为.

查看试题解析

三、解答题

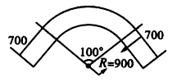
14. 弯制管道时，先按中心计算“展直长度”再下料，试计算图中所示管道的展直长度。（π≈3.14，单位：cm，精确到1cm，弯制管道的粗细不计）

查看试题解析
15. 如图1，在正方形ABCD中， $A B = 8$ ，点O与点B重合，以点O为圆心，作半径长为5的半圆O ，交AB于点E ，交AB的延长线于点F ，点M ， N是 $\overset{⌢}{E F}$ 的三等分点（点M在点N的左侧）.将半圆O绕点E逆时针旋转，记旋转角为 $α (0 ° < α \leq 90 °)$ ，旋转后，点F的对应点为点 $F^{'}$ .
图1 图2 备用图

(1)、如图2，在旋转过程中，当 $E F^{'}$ 经过点N时.
①求 $α$ 的度数；
②求图中阴影部分的面积；

(2)、在旋转过程中，若半圆O与正方形ABCD的边相切，请直接写出点A到切点的距离.

查看试题解析

四、综合题

16. 已知正方形 $A B C D$ ， $A B = 4 \sqrt{2}$ ， $E$ 是对角线上任意一点．

(1)、如图 $1$ ，以 $A E$ 为边向右作等腰直角三角形 $△ A E F$ ， $∠ E A F = 90 °$ ，连接 $D F$ ，则 $A B$ 和 $B D$ 的数量关系是；

(2)、如图 $2$ ，点 $F$ 在 $B D$ 上， $∠ E A F = 45 °$ ， $B E = 3$ ，求 $F D$ 的长为多少；

(3)、 $E$ 为 $B D$ 上任意一点 $($ 不与 $B$ ， $D$ 重合 $)$ ，作 $E P ⊥ A B$ 于 $P$ ，连接 $P D$ ， $Q$ 为 $P D$ 上一点，且 $∠ E Q D = 45 °$ ，当 $E$ 点从 $B$ 点运动到 $D$ 点时，写出 $Q$ 点运动的路径的长．

查看试题解析
17. 已知：如图，在半圆O中，直径AB的长为6，点C是半圆上一点，过圆心O作AB的垂线交线段AC的延长线于点D，交弦BC于点E.

(1)、求证：∠D＝∠ABC；

(2)、记OE＝x，OD＝y，求y关于x的函数表达式；

(3)、若OE＝CE，求图中阴影部分的面积.

查看试题解析

2023-2024学年沪科版初中数学九年级下册 24.7.1 弧长与扇形面积 同步分层训练培优卷

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年沪科版初中数学九年级下册 24.7.1 弧长与扇形面积同步分层训练培优卷