沪科版初中数学九年级下册 24.6.2 正多边形的性质 同步分层训练培优卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 正多边形的每个内角为 , 则它的边数是( )A、4 B、6 C、7 D、52. 下列命题:①各边相等的多边形是正多边形;②正多边形是轴对称图形;③正六边形的每个外角均为60°;④正n边形有(n-3)条对角线.其中真命题的个数为( )A、4 B、3 C、2 D、13. 如图,将透明直尺叠放在正五边形徽章上,若直尺的下沿于点 , 且经过点 , 上沿经过点 , 则的度数为( )
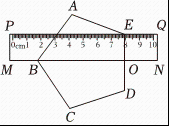 A、 B、 C、 D、4. 如图,正六边形与正方形有重合的中心O , 若∠BOC是某个正n边形的一个外角,则n的值为( )
A、 B、 C、 D、4. 如图,正六边形与正方形有重合的中心O , 若∠BOC是某个正n边形的一个外角,则n的值为( ) A、8 B、10 C、12 D、165. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为 ( )
A、8 B、10 C、12 D、165. 如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为 ( ) A、80米 B、96米 C、64米 D、48米6. 如图,点O为正六边形的中心,P,Q分别从点同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第次相遇地点的坐标为( )
A、80米 B、96米 C、64米 D、48米6. 如图,点O为正六边形的中心,P,Q分别从点同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第次相遇地点的坐标为( ) A、 B、 C、 D、7. 如图,在边长为的正八边形中,已知I,J,K,L分别是边上的动点,且满足 , 则四边形面积的最大值为( )
A、 B、 C、 D、7. 如图,在边长为的正八边形中,已知I,J,K,L分别是边上的动点,且满足 , 则四边形面积的最大值为( ) A、 B、 C、 D、8. 如图,正六边形 中,点 是边 上的点,记图中各三角形的面积依次为 ,则下列判断正确的是( )
A、 B、 C、 D、8. 如图,正六边形 中,点 是边 上的点,记图中各三角形的面积依次为 ,则下列判断正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图是第四套人民币中的菊花1角硬币,则该硬币边缘镌刻的正九边形的一个外角的度数为.
 10. 如图,直线GH与正六边形ABCDEF的边AB、EF分别交于点G、H,若∠FHG= 70°,则∠AGH=度.
10. 如图,直线GH与正六边形ABCDEF的边AB、EF分别交于点G、H,若∠FHG= 70°,则∠AGH=度. 11. 如图,正六边形螺帽的边长a=3cm,则正六边形螺帽的宽度b=
11. 如图,正六边形螺帽的边长a=3cm,则正六边形螺帽的宽度b= 12. 如图,AC,AD,CE是正五边形ABCDE的对角线,AD与CE相交于点.下列结论:
12. 如图,AC,AD,CE是正五边形ABCDE的对角线,AD与CE相交于点.下列结论:
①CF平分;②;③四边形ABCF是菱形;④
其中正确的结论是.(填写所有正确结论的序号)13. 如图,正六边形的边长为2,正六边形的外接圆与正六边形的各边相切,正六边形的外接圆与正六边形的各边相切……按这样的规律进行下去,的边长为 .
三、解答题
-
14. 已知:如图,正六边形ABCDEF的边长为6cm,延长FE,CD,相交于点G.
 (1)、求证:△FCG是正三角形.(2)、求正三角形FCG的高线长.15. 如图,O是正八边形的外接圆的圆心,M,N分别是正八边形相邻的边AB,BC上的点,且AM=BN.求∠MON的度数.
(1)、求证:△FCG是正三角形.(2)、求正三角形FCG的高线长.15. 如图,O是正八边形的外接圆的圆心,M,N分别是正八边形相邻的边AB,BC上的点,且AM=BN.求∠MON的度数.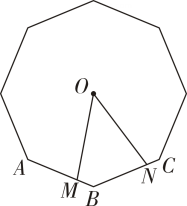
四、综合题