沪科版初中数学九年级下册 24.6.1 正多边形与圆 同步分层训练培优卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. ⊙O的半径为2,则它的内接正六边形的边长为( )A、2 B、2 C、 D、22. 如图,正九边形外接圆的半径是R,则这个正九边形的边长为( )
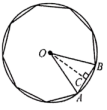 A、 B、 C、 D、3. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )
A、 B、 C、 D、3. 我国魏晋时期数学家刘微在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率的近似值为3.1416.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为( )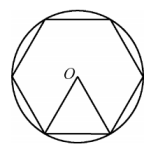 A、 B、 C、3 D、4. 如图, , 为的两条弦,连结 , , 点为的延长线上一点.若 , 则为( )
A、 B、 C、3 D、4. 如图, , 为的两条弦,连结 , , 点为的延长线上一点.若 , 则为( )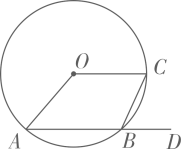 A、 B、 C、 D、5. 如图,是正六边形的边上一点,则的度数不可能是( )
A、 B、 C、 D、5. 如图,是正六边形的边上一点,则的度数不可能是( )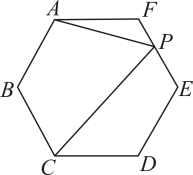 A、 B、 C、 D、6. 如图,正六边形ABCDEF内接于00,若0 O的周长等于6π,则正六边形的边长为( )
A、 B、 C、 D、6. 如图,正六边形ABCDEF内接于00,若0 O的周长等于6π,则正六边形的边长为( )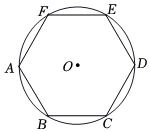 A、 B、3 C、2 D、7. ⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )A、1∶ B、 ∶ C、3∶2 D、1∶28. 以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )A、不能构成三角形 B、这个三角形是等腰三角形 C、这个三角形是直角三角形 D、这个三角形是钝角三角形
A、 B、3 C、2 D、7. ⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )A、1∶ B、 ∶ C、3∶2 D、1∶28. 以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )A、不能构成三角形 B、这个三角形是等腰三角形 C、这个三角形是直角三角形 D、这个三角形是钝角三角形二、填空题
-
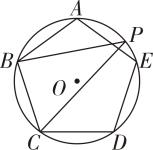
9. 如图,正五边形内接于 , 点在上,则的度数为 .
 10. 请阅读下列材料,解答问题:
10. 请阅读下列材料,解答问题:
克罗狄斯托勒密约年年 , 是希腊数学家,天文学家,地理学家和占星家.在数学方面,他还论证了四边形的特性,即有名的托勒密定理.
托勒密定理:圆的内接四边形的两条对角线的乘积等于两组对边乘积的和.
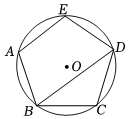
如图,正五边形内接于 , , 则对角线的长为 .
 11. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .
11. 如图,正六边形 内部有一个正五形 ,且 ,直线 经过 、 ,则直线 与 的夹角 .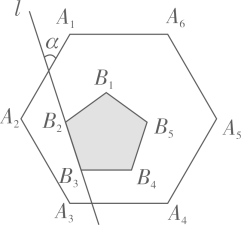 12. 观察下列结论:
12. 观察下列结论:⑴如图①,在正三角形 中,点M,N是 上的点,且 ,则 , ;
⑵如图②,在正方形 中,点M,N是 上的点,且 ,则 , ;
⑶如图③,在正五边形 中,点M,N是 上的点,且 ,则 , ;……
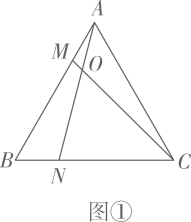
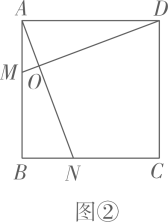
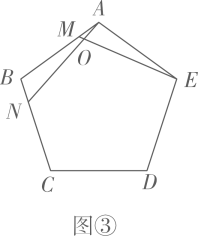
根据以上规律,在正n边形 中,对相邻的三边实施同样的操作过程,即点M,N是 上的点,且 , 与 相交于O.也会有类似的结论.你的结论是 .
三、解答题
-
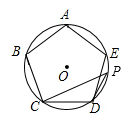
13. 我国古代数学家刘徽通过“割圆术”来估计圆周率的值——“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,可以理解为当正多边形的边数越来越多时,该正多边形与它的外接圆越来越“接近”,这样就可以用正多边形的周长替代它的外接圆的周长,从而估算出圆周率的值.(1)、对于边长为的正方形,其外接圆半径为 , 根据故事中的方法,用该正方形的周长替代它的外接圆周长,利用公式 , 可以估算.(2)、类比(1),当正多边形为正六边形时,估计的值.14. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),求 的余角的度数.
四、综合题
-
15. 如图,正方形ABCD内接于⊙O,E是 的中点,连接AE,DE,CE.
 (1)、求证:AE=DE;(2)、若CE=1,求四边形AECD的面积.16. 圆周率 的故事
(1)、求证:AE=DE;(2)、若CE=1,求四边形AECD的面积.16. 圆周率 的故事我国古代数学家刘徽通过“割圆术”来估计圆周率 的值——“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”,可以理解为当正多边形的边数越来越多时,该正多边形与它的外接圆越来越“接近”,这样就可以用正多边形的周长替代它的外接圆的周长,从而估算出圆周率 的值.
(1)、对于边长为a的正方形,其外接圆半径为 , 根据故事中的方法,用该正方形的周长4a替代它的外接圆周长,利用公式 ,可以估算 .(2)、类比(1),当正多边形为正六边形时,估计 的值.