2023-2024学年沪科版初中数学九年级下册 24.5 三角形的内切圆 同步分层训练基础卷
试卷更新日期：2024-01-29 类型：同步测试
一、选择题
-
1. 下列命题是真命题的是（ ）A、对顶角相等 B、平行四边形的对角线互相垂直 C、三角形的内心是它的三条边的垂直平分线的交点 D、三角分别相等的两个三角形是全等三角形2. 已知的内心为P，则下列说法错误的是（ ）A、 B、P在的内部 C、P为三个内角平分线的交点 D、P到三边距离相等3. 如图所示，已知⊙I是△ABC的内切圆，点I是内心，若∠A＝35°，则∠BIC等于（ ）
A、35° B、70° C、145° D、107.5°4. 下列四个命题：①直角三角形斜边上的中线等于斜边的一半；②对角线相等的平行四边形是菱形；⑨一组邻边相等的矩形是正方形；④三角形三条角平分线的交点是三角形的外心．其中真命题共有（ ）A、1个 B、2个 C、3个 D、4个5. 根据尺规作图的痕迹，可以判定点O为 的内心的是（ ）A、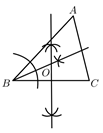
B、
C、
D、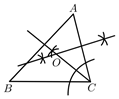
6. 如图，点O为△ABC的内心，∠B＝60°，点M，N分别为AB，且OM＝ON．甲、乙两人有如下判断：甲：∠MON＝120°：乙：当MN⊥BC时，△MON的周长有最小值．则下列说法正确的是（ ）
A、只有甲正确 B、只有乙正确 C、甲、乙都正确 D、甲、乙都错误7. 如图，锐角三角形ABC中，O为三条边的垂直平分线的交点，I为三个角的平分线的交点，若∠BOC的度为x，∠BIC的度数为y，则x、y之间的数量关系是（ ）
A、x+y＝90° B、x-2y＝90° C、x+180°＝2y D、4y-x＝360°8. 在中， ， 下列说法错误的是（ ）A、 B、 C、内切圆的半径 D、当时，是直角三角形二、填空题
-
9. 如图，△ABC中，∠BAC＝90°，∠B＝30°，BC边上有一点P（不与点B，C重合），I为△APC的内心，若∠AIC的取值范围为m°＜∠AIC＜n°，则m+n＝.
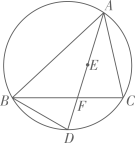
10. 如图，已知圆O为的内切圆，切点分别为D、E、F ， 且 ， ， ， 则的半径r为 ．
11. 《九章算术》中记载：“今有勾八步，股一十五步．问勾中容圆，径几何？”译文：现在有一个直角三角形，短直角边的长为8步，长直角边的长为15步．问这个直角三角形内切圆的直径是多少？书中给出的算法译文如下：如图，根据短直角边的长和长直角边的长，求得斜边的长．用直角三角形三条边的长相加作为除数，用两条直角边相乘的积再乘2作为被除数，计算所得的商就是这个直角三角形内切圆的直径．根据以上方法，求得该直径等于步．（注：“步”为长度单位）
12. 如图，已知是的内切圆， ， BO的延长线交AC于点D，若 ， ， 则的半径长为 ．
13. 如图，△ABC的三边AB，BC，CA的长度分别为3，7，8，则△ABC的内切圆Ⅰ的半径为.
三、解答题
