2023-2024学年沪科版初中数学九年级下册 24.4.3 切线长定理 同步分层训练培优卷

试卷更新日期：2024-01-29 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 如图，PA、PB是⊙O的切线，A、B为切点，若∠P=50° ， 则∠ABO的度数是（    ）

    A、25° B、35° C、45° D、50°

    查看试题解析

  • 2. 如图，PA、PB分别与⊙O相切于A、B两点，点C为⊙O上一点，连接AC、BC ， 若∠P=80° ， 则∠ACB的度数为（    ）

    A、80° B、40° C、50° D、70°

    查看试题解析

  • 3. 如图，PA，PB切⊙O 于点A，B，PA＝20，CD切⊙O于点E，交PA，PB于C，D两点，则△PCD 的周长是（   ）

    A、20 B、36 C、40 D、44

    查看试题解析

  • 4. 如图，PA、PB分别与⊙O相切于点A、B ， 连接PO并延长与⊙O交于点C、D ， 若CD=12 ， PA=8 ， 则sin∠ADB的值为（ ）

    A、45 B、35 C、34 D、43

    查看试题解析

  • 5. 如图，△ABC的内切圆⊙O与AB ， BC ， CA分别相切于点D ， E ， F ， AB=14 ， BC=13 ， CA=9 ， 则AD的长是（ ）

    A、3.5 B、4 C、4.5 D、5

    查看试题解析

  • 6. 如图，PA ， PB分别切⊙O于点A ， B ， 点C在AB上，若四边形ACBO为菱形，则∠APB为（　　）

      

    A、30° B、45° C、60° D、90°

    查看试题解析

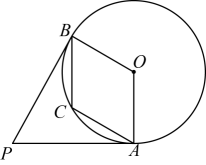  • 7. 如图，⊙O内切于正方形ABCD，边AD，CD分别与⊙O切于点E，F，点M、N分别在线段DE，DF上，且MN与⊙O相切，若△MBN的面积为8，则⊙O的半径为（   ）

    A、6 B、2 2 C、10 D、2 3

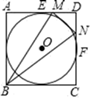    查看试题解析

  • 8. 如图，在矩形ABCD中，点E在CD边上，连接AE，将 △ADE 沿AE翻折，使点D落在BC边的点F处，连接AF，在AF上取点O，以O为圆心，线段OF的长为半径作⊙O，⊙O与AB，AE分别相切于点G，H，连接FG，GH.则下列结论错误的是（   ）

    A、∠BAE=2∠DAE B、四边形EFGH是菱形 C、AD=3CE D、GH⊥AO

    查看试题解析

二、填空题

  • 9. 如图，AB与⊙O相切于点P ， AC ， BD均为⊙O的切线，∠A=60° ， ∠ABD=90° ， AC=6 ．

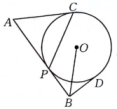    (1)、PC的长为 ．
    (2)、OB的长为 ．

    查看试题解析

  • 10. 如图，PA ， PB分别与半径为3的⊙O相切于点A ， B ， 直线CD分别交PA ， PB于点C ， D ， 并切⊙O于点E ， 当PO＝6时，△PCD的周长为 ．

    查看试题解析

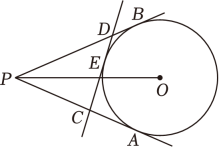  • 11. 如图，正方形ABCD的边长为4，点E是CD边上一点，连接AE，过点B作BG⊥AE于点G，连接CG并延长交AD于点F，则AF的最大值是 ．

    查看试题解析

  • 12. 如图，半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A，将直角三角板沿CA边所在的直线向左平移，当平移到AB与⊙O相切时，该直角三角板平移的距离为.

    查看试题解析

  • 13. 如图，在△ABC中，AC：BC：AB=5：12：13，⊙O在△ABC内自由移动，若⊙O的半径为1，且圆心O在△ABC内所能到达的区域的面积为 103 ，则△ABC的周长为.

    查看试题解析

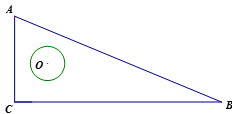
三、解答题

  • 14. 如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D的切线交BC于点E．

    (1)、求证：EB=EC；
    (2)、当△ABC满足什么条件时，四边形ODEC是正方形？证明你的结论．

    查看试题解析

  • 15. 如图，在平面直角坐标系中，点A在x轴上，以OA为直径的半圆，圆心为B ， 半径为1．过y轴上点C（0，2）作直线CD与⊙B相切于点E ， 交x轴于点D ． 二次函数y=ax2－2ax+c的图象过点C和D交x轴另一点为F点．
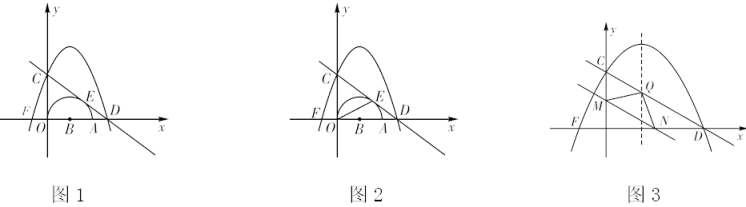    (1)、求抛物线对应的函数表达式；
    (2)、连接OE ， 如图2，求sin∠AOE的值；
    (3)、如图3，若直线CD与抛物线对称轴交于点Q ， M是线段OC上一动点，过M作MN//CD交x轴于N ， 连接QM ， QN ， 设CM=t ， △QMN的面积为S ， 求S与t的函数关系式，并写出t的取值范围．S是否存在最大值，若存在，求出最大值；若不存在，说明理由．

    查看试题解析

四、综合题

  • 16. 如图，在四边形ABCD中，AD ， 以AB为直径作⊙O ， CO平分∠BCD ， 动点P在AB左侧的半圆O上（P与点A，B均不重合）.

    (1)、求证：CD是⊙O的切线；
    (2)、记（1）中的切点为E，若AD=1 ， BC=2 ， 求sin∠APE的值.

    查看试题解析

  • 17. 我们给出以下定义：如图（1）若点P在不大于90°的∠MON的内部，作PQ⊥OM于点Q，PI⊥ON于点I，则PQ+PI称为点P与∠MON的“点角距离”记作d(P ， ∠MON).如图（2）在平面直角坐标系xoy中，x、y的正半轴组成的∠XOY ， O为坐标原点.

    (1)、如图（2）点A(4 ， 1) ， 则d(A ， ∠XOY)=；
    (2)、若点B为∠XOY内一点，d(B ， ∠XOY)=6 ， 以点B为圆心r为半径作圆，⊙B与x轴、y轴均相切，求点B的坐标；
    (3)、已知点C(2 ， 4).

    ①已知点D的坐标为(1 ， 3) ， 求OC的解析式和d(D ， ∠COY)的值.

    ②已知点E(s ， t)在∠COY的内部，d(E ， ∠COY)=255t−355s ， 当s为大于0的任意实数时，代数式mt−5s−ms+3m（m为常数）的值为定值，求m的值及该定值.

    查看试题解析