沪科版初中数学九年级下册 24.4.2 切线的判定与性质 同步分层训练基础卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
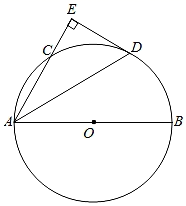
1. 如图,与相切于点 , , , 则长为( )
 A、2 B、4 C、 D、2. 如图,、是的切线,切点分别是A、B,点E在上, , 那么等于( )
A、2 B、4 C、 D、2. 如图,、是的切线,切点分别是A、B,点E在上, , 那么等于( ) A、150° B、120° C、90° D、60°3. 下列结论正确的是( )A、圆的切线垂直于半径 B、圆心角等于圆周角的2倍 C、圆内接四边形的对角互补 D、平分弦的直径垂直于这条弦4. 如图,以点P为圆心作圆,所得的圆与直线l相切的是( )
A、150° B、120° C、90° D、60°3. 下列结论正确的是( )A、圆的切线垂直于半径 B、圆心角等于圆周角的2倍 C、圆内接四边形的对角互补 D、平分弦的直径垂直于这条弦4. 如图,以点P为圆心作圆,所得的圆与直线l相切的是( ) A、以PA为半径的圆 B、以PB为半径的 C、以PC为半径的圆 D、以PD为半径的圆5. 如图,PA , PB分别与⊙O相切于A , B两点,Q是优弧上一点,若∠APB=40°,则∠AQB的度数是( )
A、以PA为半径的圆 B、以PB为半径的 C、以PC为半径的圆 D、以PD为半径的圆5. 如图,PA , PB分别与⊙O相切于A , B两点,Q是优弧上一点,若∠APB=40°,则∠AQB的度数是( )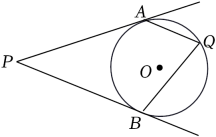 A、50° B、70° C、80° D、85°6. 在黑板上有如下内容:“如图,是半圆所在圆的直径, , 点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目.
A、50° B、70° C、80° D、85°6. 在黑板上有如下内容:“如图,是半圆所在圆的直径, , 点在半圆上,过点的直线交的延长线于点.”王老师要求添加条件后,编制一道题目.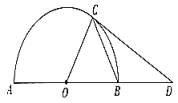
嘉嘉:若给出 , 则可证明直线是半圆的切线;
淇淇:若给出直线是的切线,且 , 则可求出的面积.
下列判断正确的是( )
A、嘉嘉和淇淇的都正确 B、只有淇淇的正确 C、嘉嘉和淇淇的都不正确 D、只有嘉嘉的正确7. 如图,在中, , , . O是边AB上一点,以点O为圆心,OA长为半径在边AB的右侧作半圆O , 交边AB于点P , 交边AC于点Q . 关于结论Ⅰ,Ⅱ,下列判断正确的是( )
结论Ⅰ:当BQ的长度最短时,半圆O的单径为
结论Ⅱ:当时,BQ与半圆O相切,且
A、只有结论Ⅰ B、只有结论Ⅱ对 C、结论Ⅰ、Ⅱ都对 D、结论Ⅰ、Ⅱ都不对8. 如图,为的切线,切点为 , 连接、 , 交于点 , 点在上,连接、 , 若 , , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,为的直径,P为延长线上的一点,过P作的切线 , A为切点, , 则的半径等于.
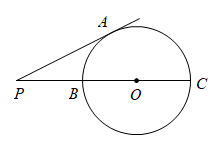 10. 如图,PA、PB分别切⊙O于点A,B,点E是⊙O上一点,且 , 则的度数为 .
10. 如图,PA、PB分别切⊙O于点A,B,点E是⊙O上一点,且 , 则的度数为 .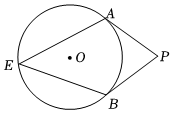 11. 如图,在 中, , , ,以点 为圆心 为半径作圆,如果 与 有唯一公共点,则半径 的值是.
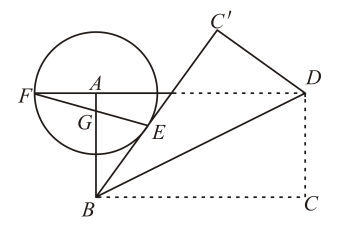
11. 如图,在 中, , , ,以点 为圆心 为半径作圆,如果 与 有唯一公共点,则半径 的值是.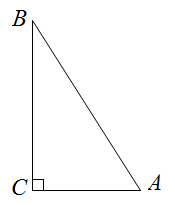 12. 在平面直角坐标系中,已知的半径为2,圆心P在抛物线上运动,当与x轴相切,且圆心P在第二象限内时,圆心P的坐标为 .13. 如图,在扇形中,点在上,连接 , 将沿折叠得到 . 若 , 且与所在的圆相切于点 , 则 .
12. 在平面直角坐标系中,已知的半径为2,圆心P在抛物线上运动,当与x轴相切,且圆心P在第二象限内时,圆心P的坐标为 .13. 如图,在扇形中,点在上,连接 , 将沿折叠得到 . 若 , 且与所在的圆相切于点 , 则 .
三、解答题
-
14. 如图,为的直径,为上一点,为上一点, , 过点作交的延长线于点 , 交于点 , 连接 , , 在的延长线上取点 , 使 .
 (1)、求证:是的切线;(2)、若的半径为 , , 求的长.15. 如图,是的外接圆,是的直径,过O作于点E , 延长至点D , 连接 , 使 .
(1)、求证:是的切线;(2)、若的半径为 , , 求的长.15. 如图,是的外接圆,是的直径,过O作于点E , 延长至点D , 连接 , 使 .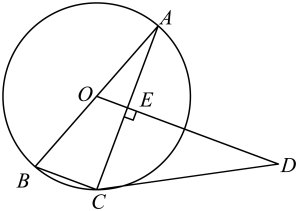 (1)、求证:是的切线;(2)、若 , 求的长.
(1)、求证:是的切线;(2)、若 , 求的长.四、综合题