2023-2024学年沪科版初中数学九年级下册 24.4.1 直线与圆的位置关系 同步分层训练培优卷

试卷更新日期：2024-01-29 类型：同步测试

进入 出卷网 下载

一、选择题

  • 1. 如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是（    ）

    A、8≤AB≤10 B、8＜AB≤10 C、4≤AB≤5 D、4＜AB≤5

    查看试题解析

  • 2. 已知⊙O的半径r=3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：

    ①若d＞5，则m=0；②若d=5，则m=1；③若1＜d＜5，则m=3；④若d=1，则m=2；⑤若d＜1，则m=4.

    其中正确命题的个数是（    ）

    A、1 B、2 C、3 D、5

    查看试题解析

  • 3. 已知⊙O的半径是一元二次方程x2−4x+4=0的解，且点O到直线AB的距离为2，则⊙O与直线AB的位置关系为（ ）．
    A、相交 B、相切 C、相离 D、无法确定

    查看试题解析

  • 4. 在Rt△ABC中，∠C=90° ， AC=3 ， BC=4 ， 以点C为圆心的⊙C的半径为2.6，则直线AB与⊙C的位置关系是（ ）
    A、相离 B、相切 C、相交 D、无法判断

    查看试题解析

  • 5. 如图，直线 y=33x+23 与x轴、y 轴分别相交于点A、B两点，圆心P的坐标为（2，0）.⊙P与y轴相切于点O，若将⊙P沿x轴向左移动，当⊙P与该直线相交时，横坐标为整数的点P的个数是（   ）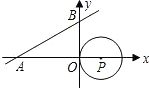

    A、5 B、6 C、7 D、8

    查看试题解析

  • 6. 如图，在平面直角坐标系xOy中，半径为2的⊙O与x轴的正半轴交于点 A ，点 B 是 ⊙O 上一动点，点 C 为弦 AB 的中点，直线 y=34x−3 与x轴、y轴分别交于点 D、E ，则 △CDE 面积的最小值为（ ）

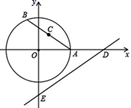    A、2 B、2.5 C、3 D、34

    查看试题解析

二、填空题

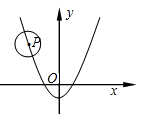
  • 7. 如图，已知 ⊙P 的半径为2，圆心P在抛物线 y=12x2−2 上运动；当 ⊙P 与x轴相切时；圆心P的坐标为.

    查看试题解析

  • 8. 初中生小明日常骑自行车上下学，某日小明沿地面一条直线骑行，自行车轮胎与这条直线的位置关系是 ． （填“相离”、“相交”或“相切”）

    查看试题解析

  • 9. 如图，在平面坐标系中， A(−2 ， 0) ， B(0 ， 1) ， C(0 ， 3) ，以O为圆心， OC 为半径画圆，P为 ⊙O 上一动点，则 32PA+PB 的最小值

    查看试题解析

  • 10. 如图，已知A点从(1 ， 0)点出发，以每秒1个单位长度的速度沿着x轴的正方向运动，经过t秒后，以O，A为顶点作菱形OABC ， 使B，C点都在第一象限内，且∠AOC=60° ， 若以P(0 ， 43)为圆心，PC为半径的圆恰好与OA所在的直线相切，则t=.

    查看试题解析

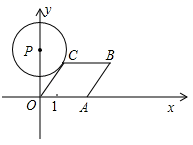
三、解答题

  • 11. 如图，已知AB是⊙O的直径，点D在⊙O上，C是⊙O外一点.若 AD//OC ，直线BC与⊙O相交，判断直线CD与⊙O的位置关系，并说明理由.

    查看试题解析

  • 12. 平面直角坐标系xOy中，点A（x1 ， y1）与B（x2 ， y2），如果满足x1+x2=0，y1﹣y2=0，其中x1≠x2 ， 则称点A与点B互为反等点．已知：点C（3，4）

    (1)、下列各点中，点C互为反等点；

    D（﹣3，﹣4），E（3，4），F（﹣3，4）

    (2)、已知点G（﹣5，4），连接线段CG，若在线段CG上存在两点P，Q互为反等点，求点P的横坐标xP的取值范围；
    (3)、已知⊙O的半径为r，若⊙O与（2）中线段CG的两个交点互为反等点，求r的取值范围．

    查看试题解析

四、综合题

  • 13. 已知：点P为图形M上任意一点，点Q为图形N上任意一点，若点P与点Q之间的距离PQ始终满足PQ＞0，则称图形M与图形N相离．

    (1)、已知点A（1，2）、B（0，-5）、C（2，-1）、D（3，4）．

    ①与直线y＝3x-5相离的点是　      　；

    ②若直线y＝3x+b与△ABC相离，求b的取值范围；

    (2)、设直线y＝3x+3、直线y＝-3x+3及直线y＝-2围成的图形为W，⊙T的半径为1，圆心T的坐标为（t，0），直接写出⊙T与图形W相离的t的取值范围．

    查看试题解析