初中数学沪科版九年级下册 24.3.2 圆内接四边形 同步分层训练基础卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
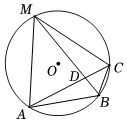
1. 如图,在的内接四边形中,点在的延长线上.若 , 则的度数是( )
 A、 B、 C、 D、2. 阿基米德折弦定理:如图1,AB与BC是⊙O的两条弦(即折线ABC是圆的一条折弦),AB>BC,点M是的中点,MN⊥AB于点N, 则点N是折弦ABC的中点, 即AN=BN+BC.如图2,半径为4的圆中有一个内接矩形ABCD, AB>BC, 点M是的中点, MN⊥AB于点N, 若矩形ABCD的面积为20,则线段BN的长为( )
A、 B、 C、 D、2. 阿基米德折弦定理:如图1,AB与BC是⊙O的两条弦(即折线ABC是圆的一条折弦),AB>BC,点M是的中点,MN⊥AB于点N, 则点N是折弦ABC的中点, 即AN=BN+BC.如图2,半径为4的圆中有一个内接矩形ABCD, AB>BC, 点M是的中点, MN⊥AB于点N, 若矩形ABCD的面积为20,则线段BN的长为( ) A、 B、 C、 D、3. 四边形ABCD的内角,∠A,∠B,∠C,∠D度数之比如下,则四边形是圆内接四边形的是( )A、4:2:2:5 B、3:1:2:5 C、4:1:1:5 D、3:1:2:44. 如图所示,四边形ABCD内接于.已知 , 则的大小是( ).
A、 B、 C、 D、3. 四边形ABCD的内角,∠A,∠B,∠C,∠D度数之比如下,则四边形是圆内接四边形的是( )A、4:2:2:5 B、3:1:2:5 C、4:1:1:5 D、3:1:2:44. 如图所示,四边形ABCD内接于.已知 , 则的大小是( ). A、 B、 C、 D、5. 如图,四边形为的内接四边形,若 , 则的度数为( )
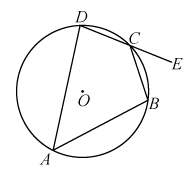
A、 B、 C、 D、5. 如图,四边形为的内接四边形,若 , 则的度数为( ) A、 B、 C、 D、6. 如图,四边形内接于 , 交的延长线于点E,若平分 , , , 则( )
A、 B、 C、 D、6. 如图,四边形内接于 , 交的延长线于点E,若平分 , , , 则( )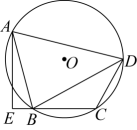 A、3 B、 C、 D、7. 如图,四边形是的内接四边形,若 , , 则所对圆心角为( )
A、3 B、 C、 D、7. 如图,四边形是的内接四边形,若 , , 则所对圆心角为( ) A、 B、 C、 D、8. 如图,半径为5的圆中有一个内接矩形 , 点是的中点,于点 , 若矩形ABCD的面积为30,则线段MN的长为( ).
A、 B、 C、 D、8. 如图,半径为5的圆中有一个内接矩形 , 点是的中点,于点 , 若矩形ABCD的面积为30,则线段MN的长为( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,四边形ABCD是⊙O的内接四边形,BE是⊙O的直径,连结CE,若∠DCE=20°, 则∠DAB= .
 10. 圆内接四边形的对角 . 如果一个平行四边形内接于圆,它必定是。11. 如图,是半径为2的的弦,将沿着弦折叠,正好经过圆心O,点C是折叠后的上一动点,连接并延长交于点D,点E是的中点,连接 , . 则的最小值为 .
10. 圆内接四边形的对角 . 如果一个平行四边形内接于圆,它必定是。11. 如图,是半径为2的的弦,将沿着弦折叠,正好经过圆心O,点C是折叠后的上一动点,连接并延长交于点D,点E是的中点,连接 , . 则的最小值为 . 12. 如图,在中, , 点D、E分别在上,且 , 将沿着折叠,点C恰好落在边上的点F处,如果 , 那么的长为
12. 如图,在中, , 点D、E分别在上,且 , 将沿着折叠,点C恰好落在边上的点F处,如果 , 那么的长为 13. 如图,四边形ABDC内接于⊙O,∠BOC=100°,则∠BAC的度数是 , ∠BDC的度数是 .
13. 如图,四边形ABDC内接于⊙O,∠BOC=100°,则∠BAC的度数是 , ∠BDC的度数是 .
三、解答题
-
14. 如图,四边形ABCD内接于⊙O,分别延长BC,AD,使它们相交于点E, , 且
 (1)、求证:(2)、若 , 点C为BE的中点,求⊙O的半径.15. 如图,已知三角形中,AB=AC,D是的外接圆劣弧AC上的点(不与点A,C重合),延长BD至E。
(1)、求证:(2)、若 , 点C为BE的中点,求⊙O的半径.15. 如图,已知三角形中,AB=AC,D是的外接圆劣弧AC上的点(不与点A,C重合),延长BD至E。 (1)、求证:AD的延长线平分(2)、若 , 中BC边上的高为 , 求外接圆的面积
(1)、求证:AD的延长线平分(2)、若 , 中BC边上的高为 , 求外接圆的面积四、综合题