2023-2024学年初中数学沪科版九年级下册 24.3.1 圆周角定理 同步分层训练培优卷
试卷更新日期：2024-01-29 类型：同步测试
一、选择题
-
1. 如图，为⊙的直径，点在圆上且在直径的两侧，若 ， 则的度数为（ ）
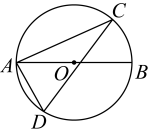A、 B、 C、 D、2. （如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC的大小是（ ）
A、30° B、45° C、60° D、70°3. 如图，在中，圆周角 ， 若P为上一点， ， 则的度数为（ ）
A、50 B、65 C、75 D、804. 如图，AB是⊙O的直径，CD是弦，AB⊥CD，垂足为点E，连接OD，CB，AC，∠DOB＝60°，EB＝2，那么CD的长为（ ）
A、 B、 C、 D、5. 如图，是的直径，点、点是上任意两点，连接 ， 若点是弧的中点， ， ， 则的面积为（ ）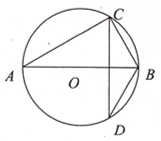
A、 B、 C、 D、6. 如图，△ 内接于⊙O， 是⊙O的直径，∠ .则∠ 的度数是 （ ）
A、36° B、33° C、30° D、27°7. 如图，在边长为8的正方形中，点O为正方形的中心，点E为边上的动点，连结 ， 作交于点F，连接 ， P为的中点，G为边上一点，且 ， 连接 ， 则的最小值为（ ）
A、10 B、 C、 D、8. 如图所示，已知在平面直角坐标系中，点A，B的坐标分别为 ， 点是轴正半轴上的一点，且满足 ， 现有以下4个结论：①的外接圆的圆心在OC上；②∠ABC=60°；③△ABC的外接圆的半径等于；④.其中正确的是（ ）.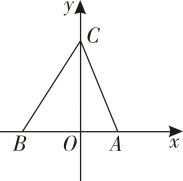
A、①② B、②③ C、③④ D、①④二、填空题
-
9. 如图，在中，弦AB ， CD相交于点P.若 ， ， 则的度数是.
10. 如图，在⊙O中，弦BC＝2，点A是圆上一点，且∠BAC＝30°，则⊙O的半径是 ．
11. 如图，AB，CD是的弦，连结AD，延长AB，CD相交于点 ， 已知 ， 则BD的度数是.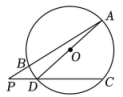
12. 已知直线l⊥AB于点E，以AB为直径画圆交直线l于点C、D，点G是弧AC上一动点，连结DG交AB于点P，连结AG并延长，交直线l于点F.若∠BAG＝45°，DP＝4，PG＝5，则AG＝ ， CD＝.
13. 如图，AB是半圆O的直径，点C在半圆上，AB＝13，AC＝12，D是上的一个动点，连接AD．过点C作CE⊥AD于E，连接BE，则BE的最小值是 ．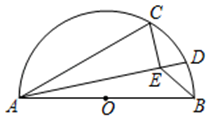
三、解答题
-
14. 如图，在平面直角坐标系xOy中，直线y＝﹣x+b与双曲线交于A ， B两点，与y轴交于点C ， 与x轴交于点D ， 其中点A的坐标为（1，3）．
(1)、求双曲线和直线AB的表达式；(2)、将直线AB向下平移，当平移后的直线A'B'与双曲线只有一个交点时，请求出直线A'B'的解析式；(3)、在y轴上是否存在点P使得∠APD＝45°？若存在，请求出点P的坐标；若不存在，请说明理由．15. 如图，AB是⊙O的直径，AB＝4，点E为弧AC的中点，连结AC，BE交于点D，过点A作AF⊥AB交BE的延长线于点F，AF＝3.
(1)、求证：AD=AF；(2)、求△ABD的周长；(3)、若点P为⊙O上一点，当△AEP为等腰三角形时，求AP的长.四、综合题
-
16. 如图，在中， ， D是上一动点，连接 ， 以为直径的交于点E ， 连接并延长交于点F ， 交于点G ， 连接 ．
(1)、求证：点B在上．(2)、当点D移动到使时，求的值．(3)、当点D到移动到使时，求证： ．17. 如图1，C，D是半圆ACB上的两点，若直径AB上存在一点P，确足∠APC＝∠BPD，则称∠CPD是的“美丽角”．
(1)、如图2，AB是⊙O的直径，弦CE⊥AB，D是上一点，连结ED交AB于点P，连结CP，∠CPD是的“美丽角”吗？请说明理由；(2)、设的度数为α，请用含α的式子表示的“美丽角”度数；(3)、如图3，在（1）的条件下，若直径AB＝5，的“美丽角”为90°，当时，求CE的长．