初中数学沪科版九年级下册 24.3.1 圆周角定理 同步分层训练基础卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 如图,△ABC是⊙O的内接三角形,∠BAC=35°,则∠BOC的度数为( )
 A、60° B、65° C、70° D、75°2. 如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子 , 在点被钉在一起,并使它们保持垂直,在测直径时,把点靠在圆周上,尺子与圆交于点 , 尺子与圆交于点 , 读得为个单位长度,为个单位长度.则圆的直径为( )
A、60° B、65° C、70° D、75°2. 如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子 , 在点被钉在一起,并使它们保持垂直,在测直径时,把点靠在圆周上,尺子与圆交于点 , 尺子与圆交于点 , 读得为个单位长度,为个单位长度.则圆的直径为( )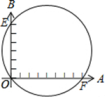 A、个单位长度 B、个单位长度 C、个单位长度 D、个单位长度3. 下列说法中,不正确的是( )A、过圆心的弦是圆的直径 B、90̊的圆周角所对的弦是直径 C、周长相等的两个圆是等圆 D、同一条弦所对的两条弧一定是等弧4. 下列命题为真命题的是( ).A、三点确定一个圆 B、度数相等的弧相等 C、90°的圆周角所对的弦是直径 D、相等的圆心角所对的弧相等,所对的弦也相等5. 如图,A,B,C,D是同一个圆上顺次任意四点,则图中相等的圆周角共有( ).
A、个单位长度 B、个单位长度 C、个单位长度 D、个单位长度3. 下列说法中,不正确的是( )A、过圆心的弦是圆的直径 B、90̊的圆周角所对的弦是直径 C、周长相等的两个圆是等圆 D、同一条弦所对的两条弧一定是等弧4. 下列命题为真命题的是( ).A、三点确定一个圆 B、度数相等的弧相等 C、90°的圆周角所对的弦是直径 D、相等的圆心角所对的弧相等,所对的弦也相等5. 如图,A,B,C,D是同一个圆上顺次任意四点,则图中相等的圆周角共有( ). A、2对 B、4对 C、6对 D、8对6. 如图,在中,弦、相交于点 , , , 则( )
A、2对 B、4对 C、6对 D、8对6. 如图,在中,弦、相交于点 , , , 则( ) A、 B、 C、 D、7. 如图,点在上, , 则( )
A、 B、 C、 D、7. 如图,点在上, , 则( )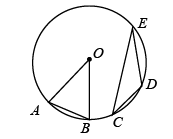 A、48° B、24° C、22° D、21°8. 如图,AB是⊙O的直径,已知 , , 那么∠COE的度数为( )
A、48° B、24° C、22° D、21°8. 如图,AB是⊙O的直径,已知 , , 那么∠COE的度数为( ) A、80° B、85° C、90° D、95°
A、80° B、85° C、90° D、95°二、填空题
-
9. 如图,A、B、D是⊙O上三点,若∠A= 30°,则∠BOD =
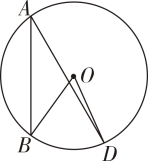 10. 如图,A,B,C,D是⊙O上四点,连结AD,AC,BD,BC.图中相等的角是(不再添加其他字母).
10. 如图,A,B,C,D是⊙O上四点,连结AD,AC,BD,BC.图中相等的角是(不再添加其他字母).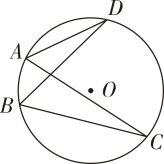 11. 如图,在中, , , 则度.
11. 如图,在中, , , 则度. 12. 如图,是的直径,弦与相交于点 , 若 , , , 则到的距离为.
12. 如图,是的直径,弦与相交于点 , 若 , , , 则到的距离为. 13. 如图,将一块含30°角的直角三角板的锐角顶点A放在⊙O上,边AB , AC分别与⊙O交于点D , E . 则的度数为 .
13. 如图,将一块含30°角的直角三角板的锐角顶点A放在⊙O上,边AB , AC分别与⊙O交于点D , E . 则的度数为 .
三、解答题
-
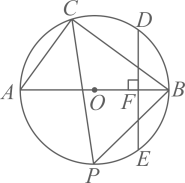
14. 如图AB是⊙O的直径,弦CD⊥AB于点E , 连接OC , 若EB=9,AE=1.
 (1)、求弦CD的长.(2)、连接AC、BC , 若∠AOC=20°,求∠BAC的度数.15. 如图,已知△ABC , 以AB为直径的半⊙O交AC于D , 交BC于E , ∠C=65°,求∠DOE的度数.
(1)、求弦CD的长.(2)、连接AC、BC , 若∠AOC=20°,求∠BAC的度数.15. 如图,已知△ABC , 以AB为直径的半⊙O交AC于D , 交BC于E , ∠C=65°,求∠DOE的度数.
四、综合题