初中数学沪科版九年级下册 24.2.4 圆的确定 同步分层训练培优卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 在Rt△ABC中,∠C=90°,AC=1cm,BC=cm,则它的外接圆直径是( ).A、1cm B、 cm C、2cm D、4cm2. 下列命题不正确的是( )A、过一点有无数个圆 B、过三点能作一个圆 C、三角形的外心是三角形三边的中垂线的交点 D、直角三角形的外接圆的直径为直角三角形的斜边3. 如图,P(x,y) 是以坐标原点为圆心、5为半径的圆周上的点.若P是整点(即x,y为整数),则这样的点共有( ).
 A、4个 B、8个 C、12个 D、16个4. 如图所示,在等腰三角形ABC中, , 按下列步骤作图:
A、4个 B、8个 C、12个 D、16个4. 如图所示,在等腰三角形ABC中, , 按下列步骤作图:
①以点为圆心、适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于为半径作弧相交于点 , 作射线AH;
②分别以A,B为圆心,大于的长为半径作弧相交于点M,N,作直线MN,交射线AH于点;
③以点为圆心、线段OA长为半径作圆.由此可得的半径为( ). A、 B、10 C、4 D、55. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( )
A、 B、10 C、4 D、55. 如图,是锐角三角形ABC的外接圆, , 垂足分别为D,E,F,连接DE,EF,FD.若的周长为21,则EF的长为( ) A、8 B、4 C、3.5 D、36. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( )
A、8 B、4 C、3.5 D、36. 如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值( ) A、4 B、8 C、10 D、67. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )
A、4 B、8 C、10 D、67. 如图,在 中, ∠ACB=90°, cm, cm. 是 边上的一个动点,连接 ,过点 作 于 ,连接 ,在点 变化的过程中,线段 的最小值是( )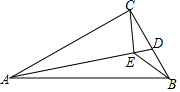 A、1 B、 C、2 D、8. 图,抛物线的图像与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( )
A、1 B、 C、2 D、8. 图,抛物线的图像与x轴交于点A,B,交y轴于点C,动点P在射线AB运动,作△BCP的外接圆⊙M,当圆心M落在该抛物线上时,则AP的值( ) A、3 B、4 C、5 D、3.5
A、3 B、4 C、5 D、3.5二、填空题
-
9. 已知直角三角形的两条直角边长分别为6cm,8cm,则此直角三角形的重心与外心之间的距离为.10. 如图,点A,B,C在同一条直线上,点D在直线AB外,过这四点中的任意3个点,能画出的圆的个数是个.
 11. 如图,是等边三角形的外接圆,其半径为4.过点B作于点E , 点P为线段上一动点(点P不与B , E重合),则的最小值为 .
11. 如图,是等边三角形的外接圆,其半径为4.过点B作于点E , 点P为线段上一动点(点P不与B , E重合),则的最小值为 .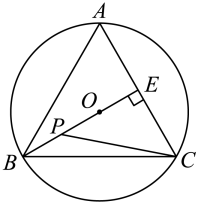 12. 已知的三个顶点都在圆O上,点O到的距离为3,且 , 则的面积= .13. 在矩形 中, , 点E在边上, , 点P为矩形内一点且 , 点M为边上一点,连接 , 则的最小值为 .
12. 已知的三个顶点都在圆O上,点O到的距离为3,且 , 则的面积= .13. 在矩形 中, , 点E在边上, , 点P为矩形内一点且 , 点M为边上一点,连接 , 则的最小值为 .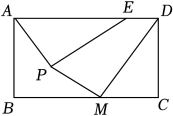
三、解答题
-
14. 在△ABC中,CE,BD分别是边AB,AC上的高,F是BC边上的中点.
 (1)、指出图中的一个等腰三角形,并说明理由.(2)、若∠A=x°,求∠EFD的度数(用含x的代数式表达).(3)、猜想∠ABC和∠EDA的数量关系,并证明.15. 已知: , 都是锐角的高.
(1)、指出图中的一个等腰三角形,并说明理由.(2)、若∠A=x°,求∠EFD的度数(用含x的代数式表达).(3)、猜想∠ABC和∠EDA的数量关系,并证明.15. 已知: , 都是锐角的高. (1)、如图 , 求证:;(2)、如图 , 延长至 , 使 , 连接 , , 过点作于点 , 在上取点 , 使 , 连接 , 求证:;(3)、如图 , 在(2)的条件下,过点作于点 , 若 , , 求线段的长.
(1)、如图 , 求证:;(2)、如图 , 延长至 , 使 , 连接 , , 过点作于点 , 在上取点 , 使 , 连接 , 求证:;(3)、如图 , 在(2)的条件下,过点作于点 , 若 , , 求线段的长.四、综合题
-
16. 在平面直角坐标系中,二次函数的图象过点和点 , 与x轴交于点A、B(点A在点B的左边),且点D与点G关于坐标原点对称.
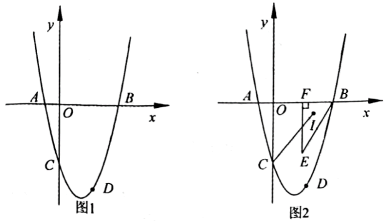 (1)、求该二次函数解析式,并判断点G是否在此函数的图象上,并说明理由;(2)、若点P为此抛物线上一点,它关于x轴,y轴的对称点分别为M,N,问是否存在这样的P点使得M,N恰好都在直线DG上?如存在,求出点P的坐标,如不存在,并说明理由;(3)、若第四象限有一动点E,满足 , 过E作轴于点F,设F坐标为 , , 的内心为I,连接CI,直接写出CI的最小值.17. 在△ABC中,AC=BC=5,tanA= , E分别是AB,AC边上的动点,作△ADE关于DE对称的图形△A′DE.
(1)、求该二次函数解析式,并判断点G是否在此函数的图象上,并说明理由;(2)、若点P为此抛物线上一点,它关于x轴,y轴的对称点分别为M,N,问是否存在这样的P点使得M,N恰好都在直线DG上?如存在,求出点P的坐标,如不存在,并说明理由;(3)、若第四象限有一动点E,满足 , 过E作轴于点F,设F坐标为 , , 的内心为I,连接CI,直接写出CI的最小值.17. 在△ABC中,AC=BC=5,tanA= , E分别是AB,AC边上的动点,作△ADE关于DE对称的图形△A′DE.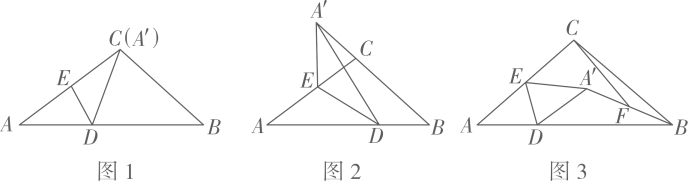 (1)、如图1,当点A′恰好与点C重合,求DE的长;(2)、如图2,当点A’落在BC的延长线上,且A’E⊥AB,求AD的长;(3)、如图3,若AE=CE,连接A’B,F是A’B的中点,连接CF,在D点的运动过程中,求线段CF长度的最大值.
(1)、如图1,当点A′恰好与点C重合,求DE的长;(2)、如图2,当点A’落在BC的延长线上,且A’E⊥AB,求AD的长;(3)、如图3,若AE=CE,连接A’B,F是A’B的中点,连接CF,在D点的运动过程中,求线段CF长度的最大值.