初中数学沪科版九年级下册 24.2.3 圆心角、弧、弦、弦心距之间的关系 同步分层训练培优卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 一条弦将圆分成1:3两部分,则劣弧所对的圆心角为( )A、30° B、60° C、90° D、120°2. 下列命题正确的是( )A、相等的圆心角所对的两条弦相等 B、圆既是中心对称图形又是轴对称图形 C、两个圆中,如果弦相等,则弦所对的圆心角也相等 D、等弧就是长度相等的弧3. 如图所示,在⊙O中, ,∠A=30°,则∠B=( )
 A、150° B、75° C、60° D、15°4. 如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( )
A、150° B、75° C、60° D、15°4. 如图,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周,P为弧AD上任意一点,若AC=5,则四边形ACBP周长的最大值是( ) A、15 B、15+5 C、20 D、15+55. 如图,已知的半径为 , 、是直径的同侧圆周上的两点, , 是的中点,动点在线段上,则的最小值为( )
A、15 B、15+5 C、20 D、15+55. 如图,已知的半径为 , 、是直径的同侧圆周上的两点, , 是的中点,动点在线段上,则的最小值为( )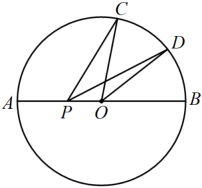 A、 B、 C、 D、6. 如图,点是的八等分点.若 , 四边形的周长分别为a,b,则下列正确的是( )
A、 B、 C、 D、6. 如图,点是的八等分点.若 , 四边形的周长分别为a,b,则下列正确的是( )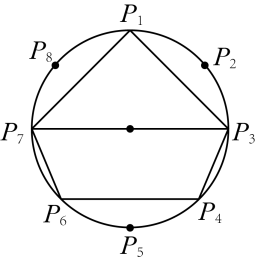 A、 B、 C、 D、a,b大小无法比较7. 如图,是半圆的直径,是弦,点是的中点,点是的中点,连接、分别交于点和点 , 连接 , 则下列结论中错误的是( )
A、 B、 C、 D、a,b大小无法比较7. 如图,是半圆的直径,是弦,点是的中点,点是的中点,连接、分别交于点和点 , 连接 , 则下列结论中错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
8. 在半径为2的中,弦的长为2,则弦所对的圆心角的度数为 .9. 如图,AB是⊙O的直径,C,D是的三等分点.若∠BOC=40°,则∠AOE的大小是 .
 10. 如图所示,AB是的直径, , 点在上,是弧MB的中点,是直径AB上的一动点,若 , 则的周长的最小值为.
10. 如图所示,AB是的直径, , 点在上,是弧MB的中点,是直径AB上的一动点,若 , 则的周长的最小值为. 11. 圆的半径为4,AB、CD是的两条弦,且 , 则最大为 .
11. 圆的半径为4,AB、CD是的两条弦,且 , 则最大为 . 12. 如图,在以AB为直径的半圆O中,C是半圆的三等分点,点P是弧BC上一动点,连接CP,AP,作OM垂直CP交AP于N,连接BN,若AB=12,则NB的最小值是 .
12. 如图,在以AB为直径的半圆O中,C是半圆的三等分点,点P是弧BC上一动点,连接CP,AP,作OM垂直CP交AP于N,连接BN,若AB=12,则NB的最小值是 .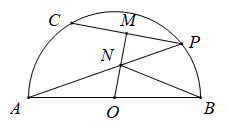
三、解答题
-
13. 如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.
 (1)、当BC=6时,求线段OD的长.(2)、求DE的长.(3)、在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.
(1)、当BC=6时,求线段OD的长.(2)、求DE的长.(3)、在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.四、综合题
-
14. 如图,已知 是⊙ 的直径,且 ,点 在半径 上(点 与点 、点 不重合),过点 作 的垂线交⊙ 于点 . 连接 ,过点 作 的平行线交⊙ 于点 ,交 的延长线于点 .
 (1)、若点 是弧BD的中点,求 的度数;(2)、求证: ;(3)、设 ,则当 为何值时 的值最大? 最大值是多少?15. 请阅读下列材料,并完成相应的任务:阿基米德折弦定理,阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯,牛顿并列为世界三大数学家.
(1)、若点 是弧BD的中点,求 的度数;(2)、求证: ;(3)、设 ,则当 为何值时 的值最大? 最大值是多少?15. 请阅读下列材料,并完成相应的任务:阿基米德折弦定理,阿基米德(公元前287年一公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯,牛顿并列为世界三大数学家.阿拉伯Al-Binmi(973年一1050年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据Al-Binmi译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
小明同学运用“截长法”和三角形全等来证明CD=AB+BD,过程如下:
证明:如图2所示,在CB上截取CG=AB,连接MA,MB,MC和MG.
∵M是的中点,∴MA=MC,…
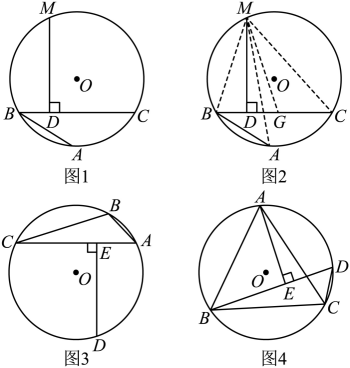 (1)、请按照上述思路,写出该证明的剩余部分;(2)、如图3,在⊙O中,BD =CD,DE⊥AC,若AB = 4,AC = 10,则AE的长度为;(3)、如图4,已知等边ABC内接于⊙O,AB = 8,D为上一点,∠ABD = 45°,AE⊥BD于点E,求BDC的周长.
(1)、请按照上述思路,写出该证明的剩余部分;(2)、如图3,在⊙O中,BD =CD,DE⊥AC,若AB = 4,AC = 10,则AE的长度为;(3)、如图4,已知等边ABC内接于⊙O,AB = 8,D为上一点,∠ABD = 45°,AE⊥BD于点E,求BDC的周长.
-