初中数学沪科版九年级下册 24.2.3 圆心角、弧、弦、弦心距之间的关系 同步分层训练基础卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 已知 是半径为6的圆的一条弦,则 的长不可能是( )A、8 B、10 C、12 D、142. 如图,点 , , , , 将的圆周进行五等分,则的度数为( )
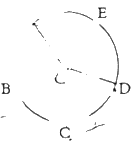 A、 B、 C、 D、3. 下列命题正确的是( )A、三个点确定一个圆 B、圆是轴对称图形,其对称轴是直径 C、90°的圆周角所对的弦是直径 D、平分弦的直径垂直于弦4. 下列图形中的角是圆心角的是( )A、
A、 B、 C、 D、3. 下列命题正确的是( )A、三个点确定一个圆 B、圆是轴对称图形,其对称轴是直径 C、90°的圆周角所对的弦是直径 D、平分弦的直径垂直于弦4. 下列图形中的角是圆心角的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,均为半径, , 下列结论不正确的是( )
5. 如图,均为半径, , 下列结论不正确的是( ) A、 B、 C、 D、6. 在⊙O中 , 则弦AB与弦CD的大小关系是( )A、AB>2CD B、AB=2CD C、AB<2CD D、AB=CD7. 如图,已知⊙O的半径为4,M是⊙O内一点,且OM=2,则过点M的所有弦中,弦长是整数的共有( )
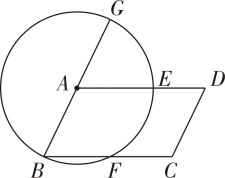
A、 B、 C、 D、6. 在⊙O中 , 则弦AB与弦CD的大小关系是( )A、AB>2CD B、AB=2CD C、AB<2CD D、AB=CD7. 如图,已知⊙O的半径为4,M是⊙O内一点,且OM=2,则过点M的所有弦中,弦长是整数的共有( ) A、1条 B、2条 C、3条 D、4条8. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( )
A、1条 B、2条 C、3条 D、4条8. 如图,AB为的直径,点D是的中点,过点D作于点E , 延长DE交于点F . 若 , , 则的直径长为( ) A、 B、8 C、10 D、
A、 B、8 C、10 D、二、填空题
-
9. 根据圆的旋转不变性,得到了圆心角与、弦、之间的关系.10. 如图,MN为⊙O的弦,∠M=55°,则∠MON的度数是
 11. ⊙O中,弦AB的长恰等于半径,则弧的度数是度.12. 直径为20cm的⊙O中,弦AB=10cm , 则弦AB所对的圆心角是 .13. 如图,AB是☉O的直径,四边形ABCD内接于☉O,OD交AC于点E,AD=CD.若AC=10,DE=4,则BC的长为 .
11. ⊙O中,弦AB的长恰等于半径,则弧的度数是度.12. 直径为20cm的⊙O中,弦AB=10cm , 则弦AB所对的圆心角是 .13. 如图,AB是☉O的直径,四边形ABCD内接于☉O,OD交AC于点E,AD=CD.若AC=10,DE=4,则BC的长为 .
三、解答题