2023-2024学年初中数学沪科版九年级下册 24.2.2 垂径定理 同步分层训练培优卷
试卷更新日期：2024-01-29 类型：同步测试
一、选择题
-
1. 如图，AB为⊙O的弦，点C在AB上，AC＝4，BC＝2，CD⊥OC交⊙O于点D，则CD的长为（ ）
A、 B、3 C、 D、2. 如图，⊙O的半径为10，弦AB＝16，点M是弦AB上的动点且点M不与点A、B重合，若OM的长为整数，则这样的点M有几个？（ ）
A、4 B、5 C、7 D、93. 如图，是弦，于点 ， 交于点 ， 若半径为5， ， 则弦的长为（ ）
A、5 B、6 C、7 D、84. 一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.6米，最深处水深0.1米，则此输水管道的半径是（ ）米
A、1 B、0.8 C、0.6 D、0.55. 如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD分别与BC，OC相交于点E，F，则下列结论不一定成立的是（ ）
A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF＝FD6. 如图，已知点C是线段AB的中点，CD⊥AB且CD＝AB＝a，延长CB至E，使得BE＝b，以CD，CE为边作矩形CEFD，连接并延长DB，交FE的延长线于点G，连接AG，《几何原本》中利用该图解释了代数式（2a+b）2+b2＝2[（a+b）2+a2]的几何意义，以AG为直径作圆，交AF于点H，若a＝9，b＝6，则HG的长为（ ）
A、5 B、18 C、3 D、177. 如图，半径为6的分别与轴，轴交于 ， 两点，上两个动点 ， ， 使恒成立，设的重心为 ， 则的最小值是（ ）
A、 B、 C、 D、8. 如图，在⊙O中，直径CD垂直弦AB于点E，且OE＝DE.点P为 上一点（点P不与点B，C重合），连结AP，BP，CP，AC，BC.过点C作CF⊥BP于点F.给出下列结论：①△ABC是等边三角形；②在点P从B→C的运动过程中， 的值始终等于 .则下列说法正确的是（ ）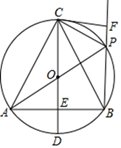
A、①，②都对 B、①对，②错 C、①错，②对 D、①，②都错二、填空题
-
9. 如图，AB是⊙O的弦，OC⊥AB于点C ， 如果 AB=8，OC=3，那么⊙O的半径等于 ．
10. 圆O的半径为5，为两条平行的弦， ． 则这两条平行弦之间的距离为 ．11. 如图，AB是⊙O的直径，弦CD⊥AB于点E，CD=AE=8cm，则OC的长为cm.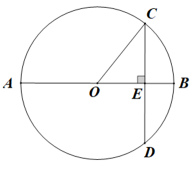
12. 在半径为1的⊙O中，弦AB、AC的长分别为1和 ，则∠BAC的度数为 ．13. 如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D两点，点E为⊙G上一动点，CF⊥AE于F，则弦AB的长度为 ；当点E在⊙G的运动过程中，线段FG的长度的最小值为 ．
三、解答题
-
14. 如图所示，在半径为的中，弦AB与CD交于点 ， ， 求CD的长.
15. 已知：如图，∠PAC=30o ， 在射线AC上顺次截取AD=3 cm，DB=10 cm，以DB为直径作⊙O，交射线AP于E、F两点，求圆心O到AP的距离及EF的长．
四、综合题
-
16. 已知点在函数的图象上．(1)、若m=-2，求n的值；(2)、抛物线与x轴交于两点M，N（M在N的左边），与y轴交于点G，记抛物线的顶点为E．
①m为何值时，点E到达最高处；②设的外接圆圆心为C，⊙C与轴的另一个交点为F，当时，是否存在四边形为平行四边形？若存在，求此时顶点E的坐标；若不存在，请说明理由．
17. 如图1，圆O的直径AB垂直弦CD于点E，点P为弧AC上的一点，连结PE并延长交圆O于点Q，连结DQ，过点P画PF∥DQ交DC的延长线于点F，若圆O的直径为10， OE=3.
(1)、求CD的长；(2)、如图2，当∠PQD=90°时，求∠PEC的正切值；(3)、如图1，设PE=x， DF=y.①求y关于x的函数解析式；②若PF×DQ=20，求y的值.