初中数学沪科版九年级下册 24.2.2 垂径定理 同步分层训练基础卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 如图,⊙O的半径为10,弦长AB=16,弦心距OC的长为( )
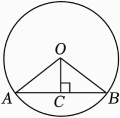 A、5 B、6 C、7 D、82. 如图,是的直径,弦于 , 若 , , 则直径的长为( )
A、5 B、6 C、7 D、82. 如图,是的直径,弦于 , 若 , , 则直径的长为( ) A、10 B、12 C、15 D、203. 下列说法正确的是( )A、垂直于弦的直线平分弦所对的两条弧 B、平分弦的直径垂直于弦 C、垂直于直径的弦平分这条直径 D、过弦(不是直径)的中点的直径平分弦所对的两条弧4. 如图所示为一名同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全升出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).
A、10 B、12 C、15 D、203. 下列说法正确的是( )A、垂直于弦的直线平分弦所对的两条弧 B、平分弦的直径垂直于弦 C、垂直于直径的弦平分这条直径 D、过弦(不是直径)的中点的直径平分弦所对的两条弧4. 如图所示为一名同学从照片上剪切下来的海上日出时的画面,“图上”太阳与海平线交于A,B两点,他测得“图上”圆的半径为10厘米,厘米.若从目前太阳所处位置到太阳完全升出海平面的时间为16分钟,则“图上”太阳升起的速度为( ).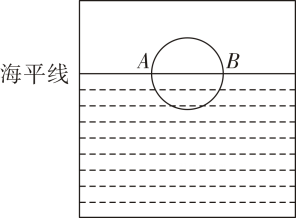 A、1.0厘米/分 B、0.8厘米/分 C、12厘米/分 D、1.4厘米/分5. 如图,是直径,弦 , 垂足为 , 若 , , 则等于( )
A、1.0厘米/分 B、0.8厘米/分 C、12厘米/分 D、1.4厘米/分5. 如图,是直径,弦 , 垂足为 , 若 , , 则等于( ) A、6 B、7 C、8 D、96. 已知,在中, , 垂足分别为相交于点 , 则的长度的最大值为( )A、2 B、 C、1 D、7. 如图,在半径为4的中,于 , 点为中点,弦的长为( )
A、6 B、7 C、8 D、96. 已知,在中, , 垂足分别为相交于点 , 则的长度的最大值为( )A、2 B、 C、1 D、7. 如图,在半径为4的中,于 , 点为中点,弦的长为( )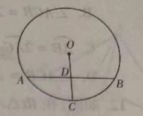 A、 B、 C、 D、8. 如图,⊙O的半径是6,AB是⊙O的弦,C是AB上一点,AC=6,BC=2,点P是⊙O上一动点,则点P与点C之间的最大距离是( )
A、 B、 C、 D、8. 如图,⊙O的半径是6,AB是⊙O的弦,C是AB上一点,AC=6,BC=2,点P是⊙O上一动点,则点P与点C之间的最大距离是( )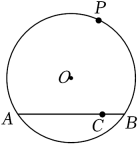 A、6+ B、12 C、6+ D、不存在
A、6+ B、12 C、6+ D、不存在二、填空题
-
9. 如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,则⊙O 的半径为cm.
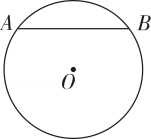 10. 如图,在中的半径 , 圆心到弦的距离为 , 则弦的长度为 .
10. 如图,在中的半径 , 圆心到弦的距离为 , 则弦的长度为 . 11. ①弦心距指圆心到圆的一条的距离.在同一个圆中,弦长越大,弦心距越小;弦长越小,弦心距.
11. ①弦心距指圆心到圆的一条的距离.在同一个圆中,弦长越大,弦心距越小;弦长越小,弦心距.②弦长、弦心距、半径这三个量中,只要知道其中的两个量,就可以求出第三个量.
12. 如图,在平面直角坐标系中,直线与相交于A,B两点,且点A在x轴上,则弦的长为.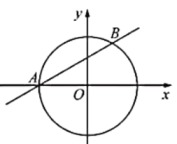 13. 如图, 是 的两条相交弦, ,则 的直径是 .
13. 如图, 是 的两条相交弦, ,则 的直径是 .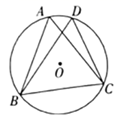
三、解答题
-
14. 点A,B,C都在⊙O上,且 , 若 , 的半径为5,连接CO,求的长.
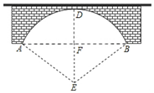
 15. 如图,某地欲搭建圆弧形拱桥,设计要求跨度AB=32米,拱高CD=8米
15. 如图,某地欲搭建圆弧形拱桥,设计要求跨度AB=32米,拱高CD=8米 (1)、求该圆弧所在圆的半径;(2)、在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩EF高度.
(1)、求该圆弧所在圆的半径;(2)、在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩EF高度.四、综合题