初中数学沪科版九年级下册 24.1.2 中心对称 同步分层训练培优卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 下列小写的希腊字母中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形:①国旗上的五角星,②有一个角为60°的等腰三角形,③一个半径为π的圆,④两条对角线互相垂直平分的四边形,⑤函数y=的图象,其中既是轴对称又是中心对称的图形有( )A、有1个 B、有2个 C、有3个 D、有4个3. 下列命题是真命题的是( )A、立方根等于它本身的数是0,1,-1 B、三角形的任意两边之和小于第三边 C、正七边形是中心对称图形 D、五边形的内角和是720°4. 勾股定理是几何学中一颗光彩夺目的明珠,现发现约有400种证明方法.下面四个图形是证明勾股定理的图形,其中既是轴对称图形又是中心对称图形的是( )A、
2. 下列图形:①国旗上的五角星,②有一个角为60°的等腰三角形,③一个半径为π的圆,④两条对角线互相垂直平分的四边形,⑤函数y=的图象,其中既是轴对称又是中心对称的图形有( )A、有1个 B、有2个 C、有3个 D、有4个3. 下列命题是真命题的是( )A、立方根等于它本身的数是0,1,-1 B、三角形的任意两边之和小于第三边 C、正七边形是中心对称图形 D、五边形的内角和是720°4. 勾股定理是几何学中一颗光彩夺目的明珠,现发现约有400种证明方法.下面四个图形是证明勾股定理的图形,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图是 的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )
5. 如图是 的网格图,将图中标有①、②、③、④的一个小正方形涂灰,使所有的灰色图形构成中心对称图形,则涂灰的小正方形是( )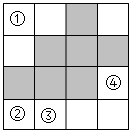 A、① B、② C、③ D、④6. 如图,在平面直角坐标系中,四边形OABC是平行四边形,且顶点的坐标为 , 点的坐标为 , 将平行四边形OABC沿着直线OC翻折,得到四边形 , 若直线把六边形的面积分成相等的两部分,则直线的解析式为( )
A、① B、② C、③ D、④6. 如图,在平面直角坐标系中,四边形OABC是平行四边形,且顶点的坐标为 , 点的坐标为 , 将平行四边形OABC沿着直线OC翻折,得到四边形 , 若直线把六边形的面积分成相等的两部分,则直线的解析式为( ) A、或 B、或 C、或 D、或7. 如图,将△ABC绕点C(0,﹣1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为( )
A、或 B、或 C、或 D、或7. 如图,将△ABC绕点C(0,﹣1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为( ) A、(﹣a,﹣b) B、(﹣a,﹣b﹣1) C、(﹣a,﹣b+1) D、(﹣a,﹣b﹣2)
A、(﹣a,﹣b) B、(﹣a,﹣b﹣1) C、(﹣a,﹣b+1) D、(﹣a,﹣b﹣2)二、填空题
-
8. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成中心对称且也以格点为顶点的三角形共有个;(不包括本身)
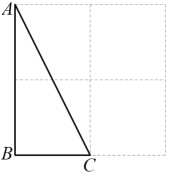 9. 如图,在平面直角坐标系中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为 , , 现平移直线l: , 使平移后的直线将这个图案分成面积相等的两个部分,则平移后直线的函数解析式为 .
9. 如图,在平面直角坐标系中,有一个由六个边长为1的正方形组成的图案,其中点A,B的坐标分别为 , , 现平移直线l: , 使平移后的直线将这个图案分成面积相等的两个部分,则平移后直线的函数解析式为 . 10. 如图,的对角线、交于点 , 则图中成中心对称的三角形共有对.
10. 如图,的对角线、交于点 , 则图中成中心对称的三角形共有对. 11. 如图,设双曲线与直线=交于,两点(点在第三象限),将双曲线在第一象限内的一支沿射线方向平移,使其经过点,将双曲线在第三象限的一支沿射线方向平移,使其经过点,平移后的两条曲线相交于,两点,此时我们称平移后的两条曲线所围部分(阴影部分)为双曲线的“眸”,为双曲线的“眸径”.当k=6时,“眸径”的长为 .
11. 如图,设双曲线与直线=交于,两点(点在第三象限),将双曲线在第一象限内的一支沿射线方向平移,使其经过点,将双曲线在第三象限的一支沿射线方向平移,使其经过点,平移后的两条曲线相交于,两点,此时我们称平移后的两条曲线所围部分(阴影部分)为双曲线的“眸”,为双曲线的“眸径”.当k=6时,“眸径”的长为 . 12. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=.
12. 在平面直角坐标系xOy中,双曲线y1= (x>0)经过平行四边形ABCD的对称中心Q,双曲线y2= (x>0,0<k<4)经过平行四边形ABCD的顶点B,C,且A(3,0),D(0,4),则k=. 13. 如图,在平面直角坐标系中,点A,B,C的坐标分别为 , , . 点M从坐标原点O出发,第一次跳跃到点 , 使得点与点O关于点A成中心对称;第二次跳跃到点 , 使得点与点关于点B成中心对称;第三次跳跃到点 , 使得点与点关于点C成中心对称;第四次跳跃到点 , 使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
13. 如图,在平面直角坐标系中,点A,B,C的坐标分别为 , , . 点M从坐标原点O出发,第一次跳跃到点 , 使得点与点O关于点A成中心对称;第二次跳跃到点 , 使得点与点关于点B成中心对称;第三次跳跃到点 , 使得点与点关于点C成中心对称;第四次跳跃到点 , 使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .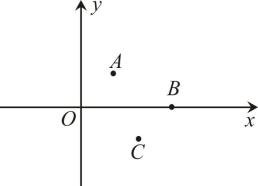
三、解答题
-
14. 在平面直角坐标系中的位置如图所示.

( 1 )作关于点C成中心对称的 .
( 2 )将向右平移个单位,作出平移后的 .
( 3 )在x轴上求作一点P,使的值最小,并求出点P的坐标.
15.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),请画出上述平移后的△A2B2C2 , 此时A2的坐标为 , C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .

四、综合题
-
16. 图①、图②均为7×6的正方形网格,点A、B、C在格点(小正方形的顶点)上.
 (1)、在图①中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;(2)、在图②中确定格点E,并画出一个以A、B、C、E为顶点的四边形,使其为中心对称图形.17. 如图,抛物线L:与x轴交于点 , 两点,与y轴交于点C,直线l经过点B和点C,点P的坐标为 .
(1)、在图①中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;(2)、在图②中确定格点E,并画出一个以A、B、C、E为顶点的四边形,使其为中心对称图形.17. 如图,抛物线L:与x轴交于点 , 两点,与y轴交于点C,直线l经过点B和点C,点P的坐标为 . (1)、求抛物线L和直线l的解析式;(2)、当点P在L上时,求m的值;(3)、过点P作y轴的平行线,分别与直线l、抛物线L交于点M、N.
(1)、求抛物线L和直线l的解析式;(2)、当点P在L上时,求m的值;(3)、过点P作y轴的平行线,分别与直线l、抛物线L交于点M、N.①当线段 , 求m的值;
②若P,M,N三点不重合,当其中两点关于第三点对称时,直接写出m的值.