2023-2024学年初中数学沪科版九年级下册 24.1.1 图形的旋转 同步分层训练培优卷
试卷更新日期：2024-01-29 类型：同步测试
一、选择题
-
1. 如图，△OAB绕点O逆时针旋转85°得到△OCD，若∠A=110°，∠D=40°，则∠α的度数是（ ）
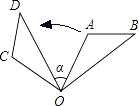A、35° B、45° C、55° D、65°2. 将如图所示的平面图形绕轴旋转一周，得到的立体图形是（ ）
A、
B、
C、
D、
3. 下列现象不属于旋转的是（ ）.A、传送带传送货物 B、飞速转动的电扇 C、钟抎的抎动 D、自行车车轮的运动4. 如图，在中， ， 将在平面内绕点旋转到的位置，使 ， 则旋转角的度数为（ ）
A、
B、
C、
D、5. 如图1，△ABC和△ADE都是等腰直角三角形，∠D和∠ACB都是直角，点C在AE上，△ABC绕着A点经过逆时针旋转后能够与△ADE重合得到图1，再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2．两次旋转的角度分别为（ ）
A、45°，90° B、90°，45° C、60°，30° D、30°，60°6. 如图，在五边形ABCDE中， ， ， 则五边形ABCDE的面积等于（ ）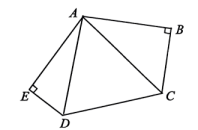
A、16 B、20 C、24 D、267. 如图，在矩形ABCD中，AB＝5，BC＝6，点E在BC边上，且BE＝2，F为AB边上的一个动点，连接EF，以EF为边作等边△EFG，且点G在矩形ABCD内，连接CG，则CG的最小值为（ ）
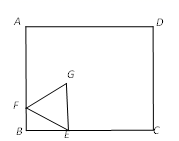A、3 B、2.5 C、4 D、28. 将边长为3的等边三角形和另一个边长为1的等边三角形如图放置（EF在边上，且点E与点B重合）．第一次将以点F为中心旋转至 ， 第二次将以点为中心旋转至的位置，第三次将以点为中心旋转至的位置，…，按照上述办法旋转，直到再次回到初始位置时停止，在此过程中的内心O点运动轨迹的长度是（ ）
A、 B、 C、 D、二、填空题
-
9. 如图，将绕着点O顺时针旋转得到 ， 若 ， 则旋转角度是 ．
10. 某正六边形的雪花图案如图所示这个图案绕着它的中心旋转一定角度后能与自身重合，则这个旋转角的大小至少为 度
11. 如图，正方形与正方形起始时互相重合，现将正方形绕点逆时针旋转．设旋转角 ， 则当时，正方形的顶点落在直线上．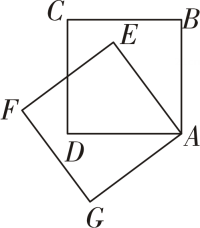
12. 如图1是一台手机支架，图2是其侧面示意图，AB、BC可分别绕点A、B转动，当AB、BC转别到∠BAE=60°，∠ABC=45°时，连结BE，∠ABE =70°，延长BC交射线AE于D．AB不动，当BC绕点B顺时针转动度或逆时针转动度时，△BDE是等腰三角形．
13. 如图，边长为3的正方形ABCD在正六边形外部做顺时针方向的滚动运动，滚动一周回到初始位置时停止，点A在滚动过程中到出发点的最大距离是.
三、解答题
-
14. 将一副直角三角板按图 1 摆放在直线 AD 上（直角三角板 OBC 和直角三角板 MON 在同一平 面内，∠OBC＝90°，∠BOC＝45°，∠MON＝90°，∠MNO＝30°），保持三角板 OBC 不动，将三 角板 MON 绕点 O 以每秒 10°的速度顺时针转动（即每一条边都绕点 O 以相同速度顺时针转动）， 转动时间为 t 秒．
(1)、当 t＝ 秒时，OM 平分∠AOC？如图 2，此时∠NOC-∠AOM＝ °；（直接写答案）(2)、继续转动三角板 MON，如图 3，使得 OM、ON 同时在直线 OC 的右侧，猜想∠NOC 与∠AOM 有怎样的数量关系？并说明理由；（数量关系中不含 t）(3)、若在三角板 MON 开始转动的同时，另一个三角板 OBC 也绕点 O 以每秒 5°的速度顺时针 转动，当 OM 旋转至射线 OD 上时同时停止，（自行画图分析）①当 t 为多少秒时，∠MOC＝15°？
②在转动过程中，请写出∠NOC 与∠AOM的数量关系，并说明理由．（数量关系中不含 t）
15. 将一副直角三角板按如图1 摆放在直线AD 上（直角三角板OBC 和直角三角板MON，∠OBC=90°，∠BOC=45°，∠MON=90°，∠MNO=30°），保持三角板OBC 不动，将三角板MON 绕点O 以每秒8°的速度顺时针方向旋转t 秒．
(1)、如图2，当t=秒时，OM 平分∠AOC，此时∠NOC﹣∠AOM=；(2)、继续旋转三角板MON，如图3，使得OM、ON 同时在直线OC 的右侧，猜想∠NOC与∠AOM 有怎样的数量关系？并说明理由（数量关系中不能含t）；(3)、直线AD 的位置不变，若在三角板MON 开始顺时针旋转的同时，另一个三角板OBC也绕点O 以每秒2°的速度顺时针旋转，当OM 旋转至射线OD 上时，两个三角板同时停止运动．①当t= 秒时，∠MOC=15°；
②请直接写出在旋转过程中，∠NOC 与∠AOM 的数量关系（数量关系中不能含t）．
四、综合题
-
16. 如图1，将一副直角三角板放在同一条直线上，其中 ， ．
(1)、观察猜想：将图1中的三角尺沿的方向平移至图2的位置，使得点O与点N重合，与相交于点E，则；(2)、操作探究：将图1中的三角尺绕点O按顺时针方向旋转，使一边在的内部，如图3，且OD恰好平分 ， 与相交于点E，求的度数；(3)、深化拓展：将图1中的三角尺绕点O按沿顺时针方向旋转一周，在旋转的过程中，当边旋转多少度时，边恰好与边平行？17. 如图，有一副直角三角板如图放置（其中 ， ）， ， 与直线重合，且三角板 ， 三角板均可以绕点逆时针旋转．
(1)、在图1中，；(2)、①如图2，若三角板保持不动，三角板绕点逆时针旋转，转速为秒，转动一周三角板就停止转动，在旋转的过程中，当旋转时间为多少时，有成立；②如图 ， 在图基础上，若三角板的边从处开始绕点逆时针旋转，转速为秒，同时三角板的边从处开始绕点逆时针旋转，转速为秒，当转到与位置重合时，两三角板都停止转动，在旋转过程中，当时，求旋转的时间是多少？