2023-2024学年初中数学沪科版八年级下册 17.5 一元二次方程的应用同步分层训练培优卷

试卷更新日期：2024-01-29 类型：同步测试

进入出卷网下载

一、选择题

1. 某校八年级组织一次篮球赛，各班均组队参赛，赛制为单循环形式（每两班之间都赛一场），共需安排15场比赛，则八年级班级的个数为（）

A、5 B、6 C、7 D、8

查看试题解析
2. 2020年~2022年无锡居民人均可支配收入由5.76万元增长至6.58万元，设人均可支配收入的平均增长率为x，下列方程正确的是（）

A、5.76( 1+x)²=6.58 B、5.76(1+x²)= 6.58 C、5.76(1+2x)= 6.58 D、5.76x²=6.58

查看试题解析
3. 我国古代著作《四元玉鉴》记载“买橡多少”问题：“六贯二百一十钱，遣人去买几株橡每株脚钱三文足，无钱准与一株椽．”其大意为现请人代买一批椽，这批椽的价钱为6 210文．如果每株椽的运费是3文，那么少拿一株椽后，剩下的橡的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为x株，则符合题意的方程是（）

A、3(x-1)x=6210 B、3(x-1)=6210 C、(3x-1)x=6210 D、3x=6 210

查看试题解析
4. 我省加快新旧动能转换，促进企业创新发展．某企业一月份的营业额是1000万元，月平均增长率相同，今年第一季度的总营业额是3640万元．若设月平均增长率是 $x$ ，那么可列出的方程是（）

A、 $1000 {(1 + x)}^{2} = 3640$ B、 $1000 (1 + 2 x) = 3640$ C、 $1000 + 1000 (1 + x) + 1000 {(1 + x)}^{2} = 3640$ D、 $1000 + 1000 (1 + x) + 1000 (1 + 2 x) = 3640$

查看试题解析
5. 某市2020年人均可支收入为2.36万元，2022年达到2.7万元，若2020年至2022年间每年人均可支配收入的增长率都为x，则下面所列方程正确的是（）

A、 $2.7 (1 + x)^{2} = 2.36$ B、 $2.36 (1 + x)^{2} = 2.7$ C、 $2.7 (1 - x)^{2} = 2.36$ D、 $2.36 (1 - x)^{2} = 2.7$

查看试题解析
6. 某农户种植花生，原来种植的花生亩产量为200千克，出油率为50％（即每100千克花生可加工成花生油50千克）．现在种植新品种花生后，每亩收获的花生可加工成花生油132千克，其中花生出油率的增长率是亩产量的增长率的 $\frac{1}{2}$ ．则新品种花生亩产量的增长率为（）

A、20％ B、30% C、50% D、120%

查看试题解析
7.
如图，若正方形OABC的顶点B和正方形ADEF的顶点E都在函数y= $\frac{1}{x}$ （x>0）的图像上，则点E的坐标为（）

A、( $\frac{1 + \sqrt{5}}{2}$ ， $\frac{\sqrt{5} - 1}{2}$ ) B、（1， $\frac{1}{2}$ ） C、（2， $\frac{1}{2}$ ） D、（ $\frac{\sqrt{2} + 1}{2}$ ， $\frac{\sqrt{2} - 1}{2}$ )

查看试题解析

二、填空题

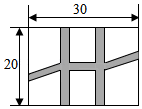
8. 新能源汽车节能、环保，越来越受消费者喜爱.2020年某款新能源汽车销售量为15万辆，销售量逐年增加，2022年预估当年销售量为21.6万辆，求这款新能源汽车的年平均增长率是多少？可设年平均增长率为x，根据题意可列方程．

查看试题解析
9. 一件商品的原价是300元，连续两次降价后，现售价是243元，若每次降价的百分率相同，那么这个百分率为．

查看试题解析
10. 如图，是一个长为30m，宽为20m的矩形花园，现要在花园中修建等宽的小道，剩余的地方种植花草.如图所示，要使种植花草的面积为468m² ，那么小道进出口的宽度应为 m.

查看试题解析
11. $《$ 代数学 $》$ 中记载，形如 $x^{2} + 8 x = 33$ 的方程，求正数解的几何方法是：“如图 $1$ ，先构造一个面积为 $x^{2}$ 的正方形，再以正方形的边长为一边向外构造四个面积为 $2 x$ 的矩形，得到大正方形的面积为 $33 + 16 = 49$ ，则该方程的正数解为 $7 - 4 = 3 .$ ”小唐按此方法解关于 $x$ 的方程 $x^{2} + 12 x = m$ 时，构造出如图 $2$ 所示的图形，已知阴影部分的面积为 $64$ ，则该方程的正数解为．

查看试题解析
12. 如图，是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a，DF＝b ，连接AE ， BE，若△ADE与△BEH的面积相等，则 $\frac{b^{2}}{a^{2}} + \frac{a^{2}}{b^{2}}$ ＝．

查看试题解析

三、解答题

13. 某租赁公司拥有汽车100辆，据统计，当每辆车的月租金为3000元时，可全部租出；每辆车的月租金每增加50元，未租出的车将会增加1辆.租出的车每辆每月需要维护费150元，未租出的车每辆每月只需要维护费50元.

(1)、当每辆车的月租金定为3600元时，能租出多少辆车？

(2)、当每辆车的月租金定为多少元时，租赁公司的月收益（租金收入扣除维护费）为306600元？

查看试题解析
14. 某扶贫单位为了提高贫困户的经济收入，购买了39m的铁栅栏，准备用这些铁栅栏为贫困户靠墙（墙长15m）围建一个中间带有铁栅栏的矩形养鸡场（如图所示）．

(1)、若要建的矩形养鸡场面积为120m² ，求鸡场的长AB和宽BC；

(2)、该扶贫单位想要建一个130m²的矩形养鸡场，这一想法能实现吗？请说明理由．

查看试题解析

四、综合题

15. 如图所示，△ABC中，∠B=90°，AB=6cm，BC=8cm.

(1)、点 P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P、Q分别从A，B同时出发，线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由.

(2)、若P点沿射线AB方向从A点出发以1cm/s的速度移动，点 Q沿射线 CB方向从C点出发以2cm/s的速度移动，P、Q同时出发，问几秒后，△PBQ的面积为1cm²？

查看试题解析
16. 已知：如图所示．在△ABC中，∠B=90°，AB=5cm ， BC=7cm ．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，当其中一点达到终点后，另外一点也随之停止运动．

(1)、如果P ， Q分别从A ， B同时出发，那么几秒后，△PBQ的面积等于4cm²？

(2)、如果P ， Q分别从A ， B同时出发，那么几秒后，PQ的长度等于5cm？

(3)、在（1）中，△PQB的面积能否等于7cm²？说明理由．

查看试题解析

2023-2024学年初中数学沪科版八年级下册 17.5 一元二次方程的应用 同步分层训练培优卷

一、选择题

二、填空题

三、解答题

四、综合题

2023-2024学年初中数学沪科版八年级下册 17.5 一元二次方程的应用同步分层训练培优卷