2023-2024学年初中数学沪科版七年级下册 7.3 一元一次不等式组 同步分层训练培优卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 不等式组的解在数轴上表示为( )A、
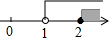 B、
B、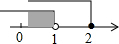 C、
C、 D、
D、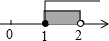 2. 若关于的不等式组无解,则的取值范围是( )A、 B、 C、 D、3. 若不等式组的解集在数轴上的表示如图所示,则这个不等式组可以是( )
2. 若关于的不等式组无解,则的取值范围是( )A、 B、 C、 D、3. 若不等式组的解集在数轴上的表示如图所示,则这个不等式组可以是( ) A、 B、 C、 D、4. 若关于x的一元一次不等式组无解,则a的取值范围是( )A、a≥1 B、a>1 C、a≤-1 D、a<-15. 关于x的不等式组恰好只有四个整数解,则a的取值范围是( )A、 B、 C、 D、6. 不等式组 的解集为x<4,则a满足的条件是( )A、a<4 B、a=4 C、a≤4 D、a≥47. 若关于的不等式组有且只有三个整数解,则的最大值是( )A、3 B、4 C、5 D、68. 关于的不等式组的最小整数解为1,则的取值范围是( )A、 B、 C、 D、或
A、 B、 C、 D、4. 若关于x的一元一次不等式组无解,则a的取值范围是( )A、a≥1 B、a>1 C、a≤-1 D、a<-15. 关于x的不等式组恰好只有四个整数解,则a的取值范围是( )A、 B、 C、 D、6. 不等式组 的解集为x<4,则a满足的条件是( )A、a<4 B、a=4 C、a≤4 D、a≥47. 若关于的不等式组有且只有三个整数解,则的最大值是( )A、3 B、4 C、5 D、68. 关于的不等式组的最小整数解为1,则的取值范围是( )A、 B、 C、 D、或二、填空题
-
9. 若关于的不等式组无解,则的取值范围是 .10. 新定义:对于实数x,我们规定 表示不大于x的最大整数,例如 , , ,如果 ,则实数x的取值范围是 .11. 已知关于的不等式组 , 下列四个结论:
若它的解集是 , 则;
当 , 不等式组有解;
若它的整数解仅有个,则的取值范围是;
若它无解,则 .
其中正确的结论是 填写序号 .12. 已知关于的不等式组的所有整数解的和为7,则的取值范围为.13. 关于的不等式组恰有四个整数解,那么的取值范围为 .三、解答题
-
14.(1)、计算:(2)、解不等式组: ,请利用数轴求不等式组的解集.
 15. 我们约定:若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“美美与共方程”,例如:方程的解为 , 而不等式组的解集为 , 不难发现在的范围内,所以方程是不等式组的“美美与共方程”.(1)、在一元一次方程①;②;③中,不等式组的“美美与共方程”是;(填序号)(2)、若关于x的方程 是不等式组的“美美与共方程”,求k的取值范围;(3)、若关于x的方程 是关于x的不等式组的“美美与共方程”,且此时该不等式组有7个整数解,若 , 求M的取值范围.
15. 我们约定:若一元一次方程的解在一元一次不等式组的解集范围内,则称该一元一次方程为该不等式组的“美美与共方程”,例如:方程的解为 , 而不等式组的解集为 , 不难发现在的范围内,所以方程是不等式组的“美美与共方程”.(1)、在一元一次方程①;②;③中,不等式组的“美美与共方程”是;(填序号)(2)、若关于x的方程 是不等式组的“美美与共方程”,求k的取值范围;(3)、若关于x的方程 是关于x的不等式组的“美美与共方程”,且此时该不等式组有7个整数解,若 , 求M的取值范围.四、综合题
-
16. 若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“友好方程”,例如:方程的解为 . 不等式组的解集为 . 因为 . 所以称方程为不等式组 , 的“友好方程”.(1)、请你写出一个方程 , 使它和不等式组为“友好方程”;(2)、若关于的方程是不等式组的“友好方程”,求的取值范围;(3)、若关于的方程是关于的不等式组的“友好方程”,且此时不等式组有3个整数解,试求的取值范围.17. 若不等式(组)①的解集中的任意解都满足不等式(组)②,则称不等式(组)①被不等式(组)②“包含”,其中不等式(组)①与不等式(组)②均有解.
例如:不等式被不等式“包含”.
(1)、下列不等式(组)中,能被不等式“包含”的是____.A、 B、 C、 D、(2)、若关于x的不等式被“包含”,若且 , 求M的最小值.(3)、已知 , , 且k为整数,关于x的不等式P: , Q: , 请分析是否存在k , 使得P和Q存在“包含”关系,且Q被P“包含”,若存在,请求出k的值,若不存在,请说明理由.