2023-2024学年初中数学沪科版七年级下册 6.2 实数 同步分层训练培优卷
试卷更新日期:2024-01-29 类型:同步测试
一、选择题
-
1. 估计的值在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间2. 如图,数轴上表示实数的点可能是( )
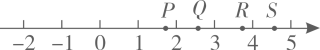 A、点P B、点Q C、点R D、点S3. 若 , 则 , , 的大小关系是( )
A、点P B、点Q C、点R D、点S3. 若 , 则 , , 的大小关系是( )
A、 B、 C、 D、4. 若 , 是两个连续的整数且 , 则( )A、8 B、7 C、6 D、55. 一个正方体的水晶砖,体积为 , 它的棱长大约在( )A、3cm与4cm之间 B、4cm与5cm之间 C、5cm与6cm之间 D、6cm与7cm之间6. 如图,在数轴上,点A表示实数a , 则a可能是( )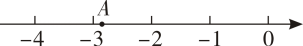 A、 B、 C、 D、7. 已知min{ , x2 , x}表示取三个数中最小的那个数,例如:当x=9,min{ , x2 , x}=min{ , 92 , 9}=3.当min{ , x2 , x}=时,则x的值为( )A、 B、 C、 D、8. 自定义运算: 例如: ,若m,n在数轴上的位置如图所示,且 ,则 的值等于( )
A、 B、 C、 D、7. 已知min{ , x2 , x}表示取三个数中最小的那个数,例如:当x=9,min{ , x2 , x}=min{ , 92 , 9}=3.当min{ , x2 , x}=时,则x的值为( )A、 B、 C、 D、8. 自定义运算: 例如: ,若m,n在数轴上的位置如图所示,且 ,则 的值等于( ) A、2028 B、2035 C、2028或2035 D、2021或2014
A、2028 B、2035 C、2028或2035 D、2021或2014二、填空题
-
9. 请写出一个比小的整数 .10. 任何实数a,可用[a]表示不超过a的最大整数,如[4]=4,[ ]=1.现对72进行如下操作:72 [ ]=8 [ ]=2 [ ]=1,这样对72只需进行3次操作后变为1,类似的,①对81只需进行次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 .11. 秦兵马俑的发现被誉为“世界第八大奇迹”,兵马俑的眼睛到下巴的距离与头顶到下巴的距离之比约为 , 则 . (选填“>”,“<”,“=”).
 12. 我们规定:表示不超过x的最大整数.如: , . 现已知对所有正整数n成立,则的值为 .13. 一个四位正整数满足百位上的数字比千位上的数字小 , 个位上的数字比十位上的数字小则称为“三五律数”,将“三五律数”的千位和十位数字组成的两位数与百位和个位数字组成的两位数的和记为 , 将“三五律数”的千位和百位数字组成的两位数与十位和个位数字组成的两位数的差记为例如:四位正整数 , , , 是“三五律数”,此时 , .(1)、四位正整数是“三五律数”,则 .(2)、若是“三五律数”,且满足是一个正整数的次方,则符合条件的为 .
12. 我们规定:表示不超过x的最大整数.如: , . 现已知对所有正整数n成立,则的值为 .13. 一个四位正整数满足百位上的数字比千位上的数字小 , 个位上的数字比十位上的数字小则称为“三五律数”,将“三五律数”的千位和十位数字组成的两位数与百位和个位数字组成的两位数的和记为 , 将“三五律数”的千位和百位数字组成的两位数与十位和个位数字组成的两位数的差记为例如:四位正整数 , , , 是“三五律数”,此时 , .(1)、四位正整数是“三五律数”,则 .(2)、若是“三五律数”,且满足是一个正整数的次方,则符合条件的为 .三、解答题
-
14. 利用如图4×4方格,作出面积为8平方单位的正方形,然后在数轴上表示实数和 .
 15. 如图,在数轴上有两个长方形ABCD和EFGH , 这两个长方形的宽都是个单位长度,长方形ABCD的长AD是个单位长度,长方形EFGH的长EH是个单位长度,点E在数轴上表示的数是 , 且E、D两点之间的距离为 .
15. 如图,在数轴上有两个长方形ABCD和EFGH , 这两个长方形的宽都是个单位长度,长方形ABCD的长AD是个单位长度,长方形EFGH的长EH是个单位长度,点E在数轴上表示的数是 , 且E、D两点之间的距离为 . (1)、点在数轴上表示的数是 , 点在数轴上表示的数是 ;(2)、若线段的中点为 , 线段上有一点N , , 点M以每秒4个单位长度的速度向右匀速运动,点N以每秒3个单位长度的速度向左运动,设运动的时间为秒,问当为多少时,原点恰为线段的三等分点?(3)、若线段的中点为 , 线段上有一点N , , 长方形以每秒4个单位长度的速度向右匀速运动,长方形保持不动,设运动时间为秒,是否存在一个的值,使以M、N、F三点为顶点的三角形是直角三角形?若存在,直接写出的值;不存在,请说明理由.
(1)、点在数轴上表示的数是 , 点在数轴上表示的数是 ;(2)、若线段的中点为 , 线段上有一点N , , 点M以每秒4个单位长度的速度向右匀速运动,点N以每秒3个单位长度的速度向左运动,设运动的时间为秒,问当为多少时,原点恰为线段的三等分点?(3)、若线段的中点为 , 线段上有一点N , , 长方形以每秒4个单位长度的速度向右匀速运动,长方形保持不动,设运动时间为秒,是否存在一个的值,使以M、N、F三点为顶点的三角形是直角三角形?若存在,直接写出的值;不存在,请说明理由.四、综合题
-
16. 下面是小李同学探索的近似数的过程:
∵面积为107的正方形边长是 , 且 ,
∴设 , 其中0<x<1,画出如图示意图,
∵图中S正方形=102+2×10•x+x2 , S正方形=107
∴102+2×10•x+x2=107
当x2较小时,省略x2 , 得20x+100≈107,得到x≈0.35,即 .
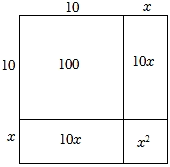 (1)、的整数部分是;(2)、仿照上述方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)17. 大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
(1)、的整数部分是;(2)、仿照上述方法,探究的近似值.(画出示意图,标明数据,并写出求解过程)17. 大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:∵ , 即 ,
∴的整数部分为2,小数部分为 .
请解答:
(1)、的整数部分是 , 小数部分是 .(2)、如果的小数部分为 , 的整数部分为 , 求的值;(3)、已知: , 其中是整数,且 , 直接写出的相反数 .