高中数学三轮复习(直击痛点):专题8向量共线定理的应用
试卷更新日期:2024-01-27 类型:三轮冲刺
一、选择题
-
1. 已知点为所在平面内一点,为平面外一点,若则的值为( )A、1 B、 C、2 D、2. 在中,点是线段上一点,点是线段上一点,且 , , 则( )A、 B、 C、 D、3. 已知平面向量和实数 , 则“”是“与共线”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. P是所在平面内一点,若 , 其中 , 则点P一定在( )A、内部 B、AC边所在的直线上 C、AB边所在的直线上 D、BC边所在的直线上5. 已知向量、满足 , , , 则一定共线的三点是( )A、A , B , D B、A , B , C C、B , C , D D、A , C , D6. 如图,在中,点 , 分别在边和边上, , 分别为和的三等分点,点靠近点 , 点靠近点 , 交于点 , 设 , , 则( )
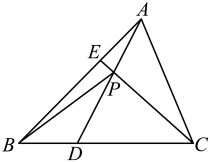 A、 B、 C、 D、
A、 B、 C、 D、二、多项选择题
-
7. 已知点 , , , , 则下列结论正确的为( )A、当时, B、当时,点在直线上 C、当时, D、当时,在方向上的投影向量的模为8. 关于平面向量,有下列四个命题,其中说法正确的是( )A、 , , 若 , 则 B、若且 , 则 C、若点G是的重心,则 D、若向量 , , 则向量在向量上的投影向量为9. 有下列说法,其中正确的说法为( )A、 , 为实数,若 , 则与共线 B、若 , , 则在上的投影向量为 C、两个非零向量 , , 若 , 则与垂直 D、若 , , 分别表示 , 的面积,则
三、填空题
-
10. 已知平面向量 , , 常数 . 向量 , 且对任意 , 总有成立,则实数的取值范围是11. 已知平面向量 , 若与共线,则的值为 .12. 已知 , 是两个不共线的向量,若与共线,则实数k的值为.
四、解答题
-
13. 如图,在中, , 点是边上一点,且 ,
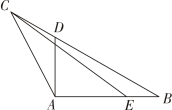 (1)、求的面积;(2)、求线段的长.14. 如图,已知的外接圆的半径为4,.
(1)、求的面积;(2)、求线段的长.14. 如图,已知的外接圆的半径为4,. (1)、求中边的长:(2)、求.15. 已知向量与的夹角为 , 且 , 是单位向量.(1)、分别求和的值;(2)、若与共线,求 .16. 向量与能作为平面向量的一组基底.(1)、若 , , , 证明三点共线(2)、若与共线,求的值17. 已知 , , 与的夹角为.(1)、若 , 求;(2)、若与垂直,求.
(1)、求中边的长:(2)、求.15. 已知向量与的夹角为 , 且 , 是单位向量.(1)、分别求和的值;(2)、若与共线,求 .16. 向量与能作为平面向量的一组基底.(1)、若 , , , 证明三点共线(2)、若与共线,求的值17. 已知 , , 与的夹角为.(1)、若 , 求;(2)、若与垂直,求.
