高中数学三轮复习（直击痛点）：专题7三角函数中的范围、最值问题

试卷更新日期：2024-01-27 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 把函数 $f (x) = s i n 2 x + \sqrt{3} c o s 2 x$ 的图象向右平移 $\frac{π}{12}$ 个单位得到函数 $g (x)$ 的图象，则函数 $g (x)$ 在区间 $[0 ， \frac{π}{2}]$ 上的值域是（）

A、[-1，1] B、[-1，2] C、[1，2] D、 $[- 2 ， 2]$

查看试题解析
2. 已知函数 $f (x) = 2 s i n ω x + 1 (ω > 0)$ 在区间 $[\frac{π}{3} ， \frac{π}{2}]$ 上是增函数，且在区间 $[0 ， π]$ 上存在唯一的 $x_{0}$ 使得 $f (x_{0}) = 3$ ，则 $ω$ 的取值不可能为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、1

查看试题解析
3. 函数 $f (x) = \sqrt{3} s i n 2 x - 2 c o s^{2} x$ 在区间 $[0 ， \frac{π}{2}]$ 上的最大值为（）

A、 $\frac{1}{2}$ B、 $\sqrt{3} - 1$ C、1 D、 $\sqrt{3}$

查看试题解析
4. 已知函数 $f (x) = a s i n 2 x + c o s 2 x + 2 (a > 0)$ 的最小值为0，则 $a =$ （）

A、1 B、2 C、3 D、 $\sqrt{3}$

查看试题解析
5. 已知 $f (x) = 3 s i n x + 2$ ，对任意的 $x_{1} \in [0$ ， $\frac{π}{2}]$ ，都存在 $x_{2} \in [0$ ， $\frac{π}{2}]$ ，使得 $f (x_{1}) = 2 f (x_{2} + θ) + 2$ 成立，则下列选项中， $θ$ 可能的值是（）

A、 $\frac{3 π}{5}$ B、 $\frac{4 π}{5}$ C、 $\frac{6 π}{5}$ D、 $\frac{7 π}{5}$

查看试题解析

二、多项选择题

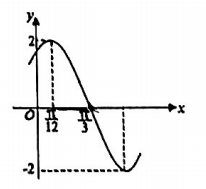
6. 已知函数， $f (x) = A s i n (ω x + φ) (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示，则（）

A、 $f (\frac{π}{2}) = - \sqrt{3}$ B、将 $y = f (x)$ 的图象向右平移 $\frac{π}{3}$ 个单位，得到 $y = A s i n x$ 的图象 C、 $\forall x_{1} ， x_{2} \in R$ ，都有 $| f (x_{1}) - f (x_{2}) | < 4$ D、若方程 $f (x) = 2 m$ 在 $[- \frac{π}{2} ， 0]$ 上有两个不相等的实数根，则实数 $m \in (- 1 ， - \frac{\sqrt{3}}{2}]$

查看试题解析
7. 已知函数 $f （ x ） = a s i n ω x + c o s ω x （ a$ 为常数， $ω > 0$ ）的图象有两条相邻的对称轴 $x = \frac{π}{6}$ 和 $x = - \frac{π}{3}$ ，则下列关于函数 $g （ x ） = s i n ω x + a c o s ω x$ 的说法正确的是（）

A、 $g （ x ）$ 的最大值为 $\sqrt{3} + 1$ B、 $g （ x ）$ 的图象关于直线 $x = \frac{π}{12}$ 对称 C、 $g （ x ）$ 在 $（ - \frac{π}{3} ， 0 ）$ 上单调递增 D、 $g （ x ）$ 的图象关于点 $（ \frac{π}{6} ， 0 ）$ 对称

查看试题解析
8. 在锐角 $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 所对的边为 $a$ ， $b$ ， $c$ ，若 $\frac{s i n B s i n C}{3 s i n A} = \frac{c o s A}{a} + \frac{c o s C}{c}$ ，且 $S_{△ A B C} = \frac{\sqrt{3}}{4} (a^{2} + b^{2} - c^{2})$ ，则 $\frac{c^{2}}{a + b}$ 的可能取值为（）

A、 $\sqrt{3}$ B、 $2$ C、 $\frac{\sqrt{14}}{2}$ D、 $\frac{3 \sqrt{10}}{5}$

查看试题解析
9. 已知函数 $f (x) = c o s^{2} x + s i n x c o s x - \frac{1}{2}$ 的图象为 $C$ ，以下说法中正确的是（）

A、函数 $f (x)$ 的最大值为 $\frac{\sqrt{2} + 1}{2}$ B、图象 $C$ 相邻两条对称轴的距离为 $\frac{π}{2}$ C、图象 $C$ 关于 $(- \frac{π}{8} ， 0)$ 中心对称 D、要得到函数 $y = \frac{\sqrt{2}}{2} s i n x$ 的图象，只需将函数 $f (x)$ 的图象横坐标伸长为原来的2倍，再向右平移 $\frac{π}{4}$ 个单位

查看试题解析

三、填空题

10. 已知函数 $f (x) = s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ .如图，直线 $y = \frac{\sqrt{3}}{2}$ 与曲线 $y = f (x)$ 交于 $A$ ， $B$ 两点， $| A B | = \frac{π}{6}$ ，则 $φ =$ =. $y = f (x)$ 在区间 $[t ， t + \frac{π}{4}] (t \in R)$ 上的最大值与最小值的差的范围是.

查看试题解析
11. 函数y=sin2x+2sinx的最大值为．

查看试题解析
12. 如图，已知函数 $f (x) = A s i n (ω x + φ)$ （其中 $A > 0$ ， $ω > 0$ ， $| φ | \leq \frac{π}{2}$ ）的图象与x轴交于点A ， B ，与y轴交于点C ， $\vec{B C} = 2 \vec{B D}$ ， $∠ O C B = \frac{π}{3}$ ， $| O A | = 2$ ， $| A D | = \frac{2 \sqrt{21}}{3}$ .则函数 $f (x)$ 在 $[1 ， 6]$ 上的值域为.

查看试题解析
13. 在 $△ A B C$ 中， $∠ C = 90 °$ ，内角 $∠ A ， ∠ A B C ， ∠ C$ 的对边分别为 $a ， b ， c$ ，且 $2 a s i n A = (2 b - \sqrt{3} c) s i n ∠ A B C + (2 c - \sqrt{3} b) s i n C$ ， $a = 1$ ，若点 $P$ 为边 $A C$ 上的动点，线段 $B P$ 的中垂线分别交直线 $B C$ 、 $A B$ 于 $E$ 、 $F$ 两点，则 $B F$ 的最小值是.

查看试题解析

四、解答题

14. 记△ABC的内角A，B，C的对边分别为a，b，c，已知b $\sin B$ +c $\sin C$ -a $\sin A$ =2b $\sin B \sin C$ ，且C≠ $\frac{π}{2}$

(1)、求证：B=A+ $\frac{π}{2}$

(2)、求cosA+sinB+sinC的取值范围.

查看试题解析
15. 已知锐角 $Δ A B C$ 的内角 $A$ ， $B$ ， $C$ ，的对边分别为 $a$ ， $b$ ， $c$ 满足 $(2 s i n A - c o s C) b = c c o s B$ ．

(1)、求 $B ；$

(2)、若 $a = 1$ ，求 $b + c$ 的取值范围．

查看试题解析
16. 已知函数 $f (x) = \sqrt{3} c o s (2 x - \frac{π}{3}) - 2 s i n x c o s x$ ．

(1)、求 $f (x)$ 的最小正周期、最大值、最小值；

(2)、求函数的单调区间．

查看试题解析
17. 已知函数f（x）＝sin（2π－x） $s i n (\frac{3 π}{2} - x) - \sqrt{3} c o s^{2} x + \sqrt{3}$

(1)、求f（x）的最小正周期和图象的对称轴方程；

(2)、当x∈ $[0 ， \frac{7 π}{12}]$ 时，求f（x）的最小值和最大值．

查看试题解析
18. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的两焦点 $F_{1} (- 1 ， 0)$ ， $F_{2} (1 ， 0)$ ，且椭圆 $C$ 过 $P (- \sqrt{3} ， \frac{\sqrt{3}}{2})$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、过点 $F_{1}$ 作不与坐标轴垂直的直线 $l$ 交椭圆 $C$ 于 $A$ ， $B$ 两点，线段 $A B$ 的垂直平分线与 $y$ 轴负半轴交于点 $Q$ ，若点 $Q$ 的纵坐标的最大值为 $- \frac{1}{8}$ ，求 $| A B |$ 的取值范围.

查看试题解析
19. 已知 $a > 0$ ，设函数 $f (x) = s i n | x + a | (x \in R)$ .

(1)、若 $a = \frac{π}{2}$ ，求函数 $f (x)$ 的单调递增区间；

(2)、试讨论函数 $f (x)$ 在 $[- a ， 2 a]$ 上的值域.

查看试题解析
20. 已知函数 $f (x) = 2 \sqrt{3} s i n x c o s x - 2 c o s^{2} x$ ．

(1)、若 $x \in R$ ，求 $f (x)$ 在 $[0 ， π]$ 的单调区间；

(2)、若 $f (x)$ 在 $[0 ， m]$ 上的最小值为 $- 2$ ，求实数m的取值范围．

查看试题解析