2023-2024学年冀教版初中数学九年级下册 30.5 二次函数与一元二次方程的关系同步分层训练培优题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 若函数的图象与轴只有一个交点,则的值是( )A、或 B、 C、 D、2. 如图,二次函数y=ax2+bx+c的图象经过点A(1,0),B(5,0),下列说法正确的是( )
 A、c<0 B、b2-4ac<0 C、a-b+c<0 D、图象的对称轴是直线x=33. 如图,抛物线与x轴负半轴,y轴分别交于点A , B , 现要在段的抛物线上找点 , 关于针对n的不同取值,所找点P的个数,甲、乙两人的说法如下,下列判断正确的是( )
A、c<0 B、b2-4ac<0 C、a-b+c<0 D、图象的对称轴是直线x=33. 如图,抛物线与x轴负半轴,y轴分别交于点A , B , 现要在段的抛物线上找点 , 关于针对n的不同取值,所找点P的个数,甲、乙两人的说法如下,下列判断正确的是( )甲:若 , 则点P的个数为2;乙:若 , 则点P的个数为1
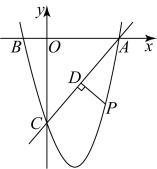
 A、只有甲对 B、只有乙对 C、甲、乙都对 D、甲、乙都不对4. 题目:“如图,抛物线与直线相交于点和点B.点M是直线AB上的一个动点,将点M向左平移3个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.”对于其答案,甲答: , 乙答: , 丙答: , 丁答: , 则正确的是( )
A、只有甲对 B、只有乙对 C、甲、乙都对 D、甲、乙都不对4. 题目:“如图,抛物线与直线相交于点和点B.点M是直线AB上的一个动点,将点M向左平移3个单位长度得到点N,若线段MN与抛物线只有一个公共点,直接写出点M的横坐标的取值范围.”对于其答案,甲答: , 乙答: , 丙答: , 丁答: , 则正确的是( )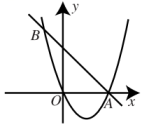 A、只有甲答的对 B、甲、乙答案合在一起才完整 C、甲、丙答案合在一起才完整 D、甲、丁答案合在一起才完整5. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法不正确的是( )
A、只有甲答的对 B、甲、乙答案合在一起才完整 C、甲、丙答案合在一起才完整 D、甲、丁答案合在一起才完整5. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法不正确的是( )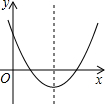 A、b2﹣4ac>0 B、a>0 C、c>0 D、6. 已知多项式 , 下列说法正确的个数为( )
A、b2﹣4ac>0 B、a>0 C、c>0 D、6. 已知多项式 , 下列说法正确的个数为( )若 , 则代数式的值为; 当时,代数式的最小值为; 当时,若 , 则的取值范围是 .
A、个 B、个 C、个 D、个7. 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,1),(0,3)之间(包含端点).现有下列结论:
①当x<-1时,y<0;
②3a +b+2c>0;
③-1≤a≤
④3≤n≤4.
其中正确的有( ).
A、①③ B、②③ C、①②③ D、①②④8. 如图所示,二次函数的图象与轴交于A,B两点,与轴正半轴交于点 , 它的对称轴为直线.下列选项中,正确的是( ). A、 B、 C、 D、当(为实数)时,
A、 B、 C、 D、当(为实数)时,二、填空题
-
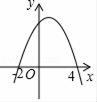
9. 若函数y=ax2﹣x+1(a为常数)的图象与x轴只有一个交点,那么那么a的值是 .10. 如图,二次函数y=ax2+bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是
 11. 如图,抛物线与x轴交于A , B两点,P是以点为圆心,2cm为半径的圆上的动点,Q是线段PA的中点,连接OQ , 则线段OQ的最大值是.
11. 如图,抛物线与x轴交于A , B两点,P是以点为圆心,2cm为半径的圆上的动点,Q是线段PA的中点,连接OQ , 则线段OQ的最大值是.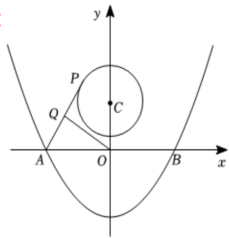 12. 抛物线y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标为-5和1,则方程ax2-bx+c=0的解为 .13. 如图,抛物线与x轴交于点A,B,与y轴交于点C,点在抛物线上,点E在直线上,若 , 则点E的坐标是 .
12. 抛物线y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标为-5和1,则方程ax2-bx+c=0的解为 .13. 如图,抛物线与x轴交于点A,B,与y轴交于点C,点在抛物线上,点E在直线上,若 , 则点E的坐标是 .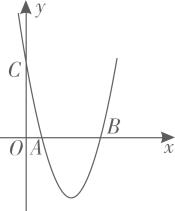
三、解答题
-
14. 如图,二次函数的图象与x轴相交于点A(-1,0)和B(m , 0),与y轴相交于点C , 且经过点D(3,3),过点D作DE⊥BD , 交y轴于点E , 连结BE .
 (1)、当m=6时,求这个二次函数的表达式.(2)、试用含m的代数式表示点C的坐标.(3)、作点D关于BE的对称点D′ , 连结OD′ , ED′ . 当△OD′E的面积等于1时,请直接写出m的值.15. 如图.取某一位置的水平线为x轴.建立平面直角坐标系后,小山坡AB可近似地看成抛物线:的一部分.小球在离点A3m的点C处抛出.落在山坡的点D处(点D在小山坡AB的坡顶的右侧),小球的运动轨迹为抛物线:的一部分.
(1)、当m=6时,求这个二次函数的表达式.(2)、试用含m的代数式表示点C的坐标.(3)、作点D关于BE的对称点D′ , 连结OD′ , ED′ . 当△OD′E的面积等于1时,请直接写出m的值.15. 如图.取某一位置的水平线为x轴.建立平面直角坐标系后,小山坡AB可近似地看成抛物线:的一部分.小球在离点A3m的点C处抛出.落在山坡的点D处(点D在小山坡AB的坡顶的右侧),小球的运动轨迹为抛物线:的一部分. (1)、求小山坡AB的坡顶高度;(2)、若测得点D的高度为3m,求抛物线的函数解析式(不要求写自变量x的取值范围);(3)、当小球运动到坡顶正上方,且与坡顶距离超过3米时,请直接写出b的取值范围.
(1)、求小山坡AB的坡顶高度;(2)、若测得点D的高度为3m,求抛物线的函数解析式(不要求写自变量x的取值范围);(3)、当小球运动到坡顶正上方,且与坡顶距离超过3米时,请直接写出b的取值范围.四、综合题