2023-2024学年冀教版初中数学九年级下册 30.5 二次函数与一元二次方程的关系同步分层训练基础题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 抛物线 $y = - 3 x^{2} - x + 4$ 与x轴的交点个数是（）

A、3 B、2 C、1 D、0

查看试题解析
2. 抛物线 $y = {(1 - x)}^{2}$ 与 $y$ 轴的交点坐标为（）

A、 $(1 ， 0)$ B、 $(- 1 ， 0)$ C、 $(0 ， 1)$ D、 $(0 ， - 1)$

查看试题解析
3. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则函数值 $y < 0$ 时x的取值范围是（）

A、 $x < - 1$ B、x＞3 C、－1＜x＜3 D、 $x < - 1$ 或x＞3

查看试题解析
4. 下表是二次函数y=ax²+bx+c的自变量x与函数值y的对应值表．由表中数据可判断，方程ax²+bx+c=0(a≠0，a，b，c为常数)的一个解x的取值范围是（）．
x
6.17
6.18
6.19
6.20
y=ax²+bx+c
-0.03
-0.01
0.02
0.04

A、6<x<6.17 B、6.17<x<6.18 C、6.18<x<6.19 D、6.19<x<6.20

查看试题解析
5. 二次函数 $y = x^{2} + b x + c$ 的部分对应值如表则一元二次方程 $x^{2} + b x + c = 0$ 的解为（）
$x$
.…
-2
-1
0
1
2
4
…
$y$
…
5
0
-3
-4
-3
5
…

A、 $x_{1} = - 1$ ， $x_{2} = - 3$ B、 $x_{1} = - 1$ ， $x_{2} = 1$ C、 $x_{1} = - 1$ ， $x_{2} = 3$ D、 $x_{1} = - 1$ ， $x_{2} = 5$

查看试题解析
6. 已知二次函数 $y = x^{2} + 2 x + m$ 的部分图象如图所示，则关于x的一元二次方程 $x^{2} + 2 x + m = 0$ 的解为（）

A、 $x_{1} = 3$ ， $x_{2} = 1$ B、 $x_{1} = - 3$ ， $x_{2} = 1$ C、 $x_{1} = - 3$ ， $x_{2} = 3$ D、 $x_{1} = - 3$ ， $x_{2} = - 1$

查看试题解析
7. 抛物线y＝kx²﹣7x﹣7的图象和x轴有交点，则k的取值范围是（）

A、k＞﹣ $\frac{7}{4}$ B、k≥﹣ $\frac{7}{4}$ 且k≠0 C、k≥﹣ $\frac{7}{4}$ D、k＞﹣ $\frac{7}{4}$ 且k≠0

查看试题解析
8. 如图所示的是二次函数y＝ax²+bx+c的部分图象，由图象可知不等式ax²+bx+c＜0的解集是（　　）

A、-1＜x＜5 B、x＞5 C、x＜-1且x＞5 D、x＜-1或x＞5

查看试题解析

二、填空题

9. 二次函数 $y = - (x + 1)^{2} - 2$ 与 $y$ 轴的交点坐标是．

查看试题解析
10. 抛物线 $y = x^{2} + 2 x + c$ 与x轴只有一个公共点，则c的值为.

查看试题解析
11. 二次函数y=a(x+5)(x-3)的图象如图所示，当y>0时，x的取值范围是.

查看试题解析
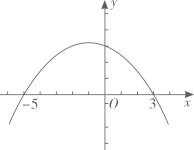12. 函数 $y = x^{2} - 2 x - 2$ 的图象如图所示，根据其中提供的信息，可求得方程 $x^{2} - 2 x - 2 = 1$ 的解是．

查看试题解析
13. 我们约定： $(a ， b ， c)$ 为函数 $y = a x^{2} + b x + c$ 的关联数，当其图象与坐标轴交点的横、纵坐标均为整数时，该交点为“整交点”，若关联数为 $(m ， - m - 2 ， 2)$ 的函数图象与x轴有两个整交点（m为正整数），则这个函数图象上整交点的坐标为.

查看试题解析

三、解答题

14. 如图，已知二次函数y＝x²+bx+c图象经过点A（1，﹣2）和B（0，﹣5）．

(1)、求该二次函数的表达式及图象的顶点坐标；

(2)、当y≤﹣2时，请根据图象直接写出x的取值范围．

查看试题解析
15. 如图，已知抛物线的顶点为A（1，4），抛物线与y轴交于点B（0，3），与x轴交于C、D两点．

(1)、求此抛物线的解析式；

(2)、求△BCD的面积．

查看试题解析

四、综合题

16. 新定义：[a，b，c]为二次函数y=ax²+bx+e（a≠0，a，b，c为实数）的“图象数”，如：y=-x²+2x+3的“图象数”为[-1，2，3]

(1)、二次函数y= $\frac{1}{3}$ x²-x-1的“图象数”为．

(2)、若图象数”是[m，m+1，m+1]的二次函数的图象与x轴只有一个交点，求m的值．

查看试题解析
17. 如图所示，在平面直角坐标系中，二次函数 $y = a x^{2} + 4 x - 3$ 的图象的顶点是 $A$ ，与 $x$ 轴交于B，C两点，与 $y$ 轴交于点 $D$ .点 $B$ 的坐标是 $(1 ， 0)$ .

(1)、求A，C两点的坐标，并根据图象直接写出当 $y > 0$ 时 $x$ 的取值范围.

(2)、平移该二次函数的图象，使点 $D$ 恰好落在点 $A$ 的位置上，求平移后的图象所对应的二次函数的表达式.

查看试题解析

x	6.17	6.18	6.19	6.20
y=ax²+bx+c	-0.03	-0.01	0.02	0.04

$x$	.…	-2	-1	0	1	2	4	…
$y$	…	5	0	-3	-4	-3	5	…