2023-2024学年冀教版初中数学九年级下册 30.4 二次函数的应用同步分层训练培优题

试卷更新日期：2024-01-27 类型：同步测试

进入出卷网下载

一、选择题

1. 用一段 $20$ 米长的铁丝在平地上围成一个长方形，求长方形的面积 $y$ （平方米）和长方形的一边的长 $x$ （米）的关系式为（）

A、 $y = - x^{2} + 20 x$ B、 $y = x^{2} - 20 x$ C、 $y = - x^{2} + 10 x$ D、 $y = x^{2} - 10 x$

查看试题解析
2. 如图，一座抛物线型拱桥，桥下水面宽度是6m时，拱顶到水面的距离是3m ，则当水面宽为4m时，水面上升了（　　）

A、 $\frac{1}{3}$ m B、1m C、 $\frac{4}{3}$ m D、 $\frac{5}{3}$ m

查看试题解析
3. 共享单车为市民出行带来了方便，某单车公司第一个月投放 $a$ 辆单车，计划第三个月投放单车 $y$ 辆，若第二个月的增长率是 $x$ ，第三个月的增长率是第二个月的两倍，那么 $y$ 与 $x$ 的函数关系是（）

A、 $y = a (1 + x) (1 + 2 x)$ B、 $y = a {(1 + x)}^{2}$ C、 $y = 2 a {(1 + x)}^{2}$ D、 $y = 2 x^{2} + a$

查看试题解析
4.
竖直向上发射的小球的高度h（m）关于运动时间t（s）的函数表达式为h=at²+bt，其图象如图所示，若小球在发射后第2秒与第6秒时的高度相等，则下列时刻中小球的高度最高的是（　　）

A、第3秒 B、第3.5秒 C、第4.2秒 D、第6.5秒

查看试题解析
5. 某班计划在劳动实践基地内种植蔬菜，班长买回来10米长的围栏，准备围成两边靠墙（两墙垂直且足够长）的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形、等腰直角三角形（两直角边靠墙）、扇形这三种方案，如图所示．最佳方案是（）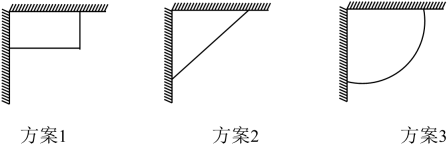

A、方案1 B、方案2 C、方案1或方案2 D、方案3

查看试题解析
6. 如图，等边 $△ A B C$ 的边长为4，直线l经过点A且直线 $l ⊥ A C$ ，直线l从点A出发沿A-C以1cm/s的速度向点C移动，直到经过点C即停止，直线l分别与AB或BC交于点M ，与AC交于点N ，若 $△ A M N$ 的面积为y（cm $^{2}$ ），直线l的移动时间为x（s），则下面最能反映y与x之间函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
7. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 15$ ， $B C = 20$ ．点 $D$ 从点 $A$ 出发沿折线 $A - C - B$ 运动到点 $B$ 停止，过点 $D$ 作 $D E ⊥ A B$ ，垂足为 $E$ ．设点 $D$ 运动的路径长为 $x$ ， $△ B D E$ 的面积为 $y$ ，若 $y$ 与 $x$ 的对应关系如图所示，则 $a - b$ 的值为（）

A、54 B、52 C、50 D、48

查看试题解析
8. 如图，在平面直角坐标系中，抛物线 $y = - x^{2} - 4 x + 1$ 与 $y$ 轴交于点 $A$ ，过点 $A$ 平行于 $x$ 轴的直线交抛物线 $y = x^{2}$ 于 $B$ 、 $C$ 两点，点 $P$ 在抛物线 $y = - x^{2} - 4 x + 1$ 上且在 $x$ 轴的上方，连接 $P B$ ， $P C$ 则 $△ P B C$ 面积的最大值是（）

A、5 B、4.5 C、6 D、4

查看试题解析

二、填空题

9. 如图，用一段长为16m的篱笆围成一个一边靠墙的矩形围栏（墙足够长），则这个围栏的最大面积为m².

查看试题解析
10. 超市购进一批单价为40元的生活用品，如果按每件50元出售，那么每天可销售200件，经调查发现，这种生活用品的销售单价每提高1元，其销售量相应减少10件，则超市销售此生活用品每天可获得最大销售利润为元．

查看试题解析
11. 一个小球从地面竖直向上弹出，它在空中距离地面的高度 $h (m)$ 与弹出时间 $t (s)$ 满足的关系式为 $h = 15 t - 5 t^{2}$ ，当小球第二次距离地面 $10 m$ 时，小球弹出的时间为秒.

查看试题解析
12. 二次函数 $y = a (x - 1) (x - 5) (a > \frac{1}{2})$ 的图像与x轴交于点 $A$ 、 $B$ ，与 $y$ 轴交于点 $C$ ，过点 $M (3 ， 1)$ 的直线将 $△ A B C$ 分成两部分，这两部分是三角形或梯形，且面积相等，则 $a$ 的值为．

查看试题解析
13. 如图，在矩形 $A B C D$ 中， $A B = 10$ ， $B C = 5$ ，点P从点A出发，沿线段 $A D$ 以每秒1个单位长度的速度向终点D运动；点Q从点B出发，沿线段 $B A$ 以每秒2个单位长度的速度向终点A运动． P ， Q两点同时出发，设点P运动的时间为 $t$ （单位：秒）， $△ A P Q$ 的面积为 $y$ ．则 $y$ 关于 $t$ 的函数表达式为．

查看试题解析

三、解答题

14. 2023年亚运会已在杭州举行，在这期间某网络经销商购进一批以亚运会为主题的文化衫进行销售，文化衫的进价为每件40元，当销售单价定为70元时，每天可售出50件．为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，则每天可多售出5件，若设这款文化衫降低了x（元），每天的销售量为y（件）．

(1)、请直接写出y与x之间的函数关系式和自变量x的取值范围．

(2)、当销售单价为多少元时，销售每天所获得的利润为1875元？

(3)、当销售单价定为多少元时，每天销售这款文化纪念册获得的利润w最大？最大利润是多少元？

查看试题解析

四、综合题

15. 如图1，在平面直角坐标系中，正方形OABC的边长为4，边OA ， OC分别在x轴，y轴的正半轴上，把正方形OABC的内部及边上，横、纵坐标均为整数的点称为好点．点P为抛物线y＝﹣（x﹣m）²+m+2的顶点．

(1)、直接写出顶点P的坐标；（用m表示）

(2)、当m＝0时，判断（1，1）是否在抛物线上，并直接写出该抛物线下方（含边界）的好点个数；

(3)、当m＝3时，直接写出该抛物线上的好点坐标；

(4)、若点P在正方形OABC内部，该抛物线下方（含边界）恰好存在8个好点，直接写出m的取值范围．

查看试题解析