2023-2024学年冀教版初中数学九年级下册 30.4 二次函数的应用同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
 A、y=
A、y=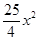 B、y=﹣
B、y=﹣ 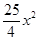 C、y=﹣
C、y=﹣ 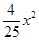 D、y=
D、y= 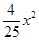 2. 一小球被抛出后,距离地面的高度和飞行时间满足+6,则小球距离地面的最大高度是( ).A、 B、 C、 D、3. 小明在期末体育测试中掷出的实心球的运动路线呈抛物线形,若实心球运动的抛物线的解析式为y=-(x-3)2+k,其中y是实心球飞行的高度,x是实心球飞行的水平距离,已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为( )
2. 一小球被抛出后,距离地面的高度和飞行时间满足+6,则小球距离地面的最大高度是( ).A、 B、 C、 D、3. 小明在期末体育测试中掷出的实心球的运动路线呈抛物线形,若实心球运动的抛物线的解析式为y=-(x-3)2+k,其中y是实心球飞行的高度,x是实心球飞行的水平距离,已知该同学出手点A的坐标为(0,),则实心球飞行的水平距离OB的长度为( )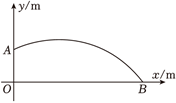 A、7m B、7.5m C、8m D、8.5m4. 已知实心球运动的高度与水平距离之间的函数关系是 , 则该同学此次投掷实心球的成绩是( )
A、7m B、7.5m C、8m D、8.5m4. 已知实心球运动的高度与水平距离之间的函数关系是 , 则该同学此次投掷实心球的成绩是( )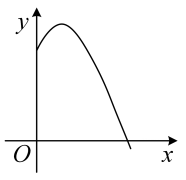 A、 B、 C、 D、5. 如图,等腰直角三角形ABC中,∠A=90°,BC=8,点D、点E分别是BC、AC边上的点,DE//AB则S△BDE的最大值是( )
A、 B、 C、 D、5. 如图,等腰直角三角形ABC中,∠A=90°,BC=8,点D、点E分别是BC、AC边上的点,DE//AB则S△BDE的最大值是( )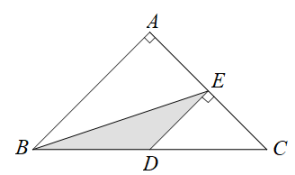 A、3 B、4 C、5 D、66. 某商场第1年销售计算机5000台,如果每年的销售量比上一年增加相同的百分率x , 第3年的销售量为y台,则y关于x的函数解析式为( )A、y=5000(1+2x) B、y=5000(1+x)2 C、y=5000+2x D、y=5000x27. 如图,一位篮球运动员投篮,球的行进路线是沿抛物线( , 的单位都为),然后准确落入篮筐内,已知篮筐的中心离地面的高度为 , 他距篮筐中心的水平距离是 , 则的值为( ).
A、3 B、4 C、5 D、66. 某商场第1年销售计算机5000台,如果每年的销售量比上一年增加相同的百分率x , 第3年的销售量为y台,则y关于x的函数解析式为( )A、y=5000(1+2x) B、y=5000(1+x)2 C、y=5000+2x D、y=5000x27. 如图,一位篮球运动员投篮,球的行进路线是沿抛物线( , 的单位都为),然后准确落入篮筐内,已知篮筐的中心离地面的高度为 , 他距篮筐中心的水平距离是 , 则的值为( ).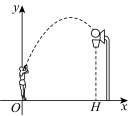 A、 B、 C、 D、8. 某大桥的桥拱可以用抛物线的一部分表示,函数关系为 , 当水面宽度AB为20m时,水面与桥拱顶的高度CO等于 ( )
A、 B、 C、 D、8. 某大桥的桥拱可以用抛物线的一部分表示,函数关系为 , 当水面宽度AB为20m时,水面与桥拱顶的高度CO等于 ( )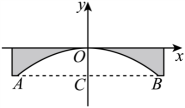 A、2m B、4m C、10m D、16m
A、2m B、4m C、10m D、16m二、填空题
-
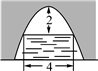
9. 小明推铅球时,若铅球的高度与水平距离之间的关系为 , 则小明推铅球的成绩是m.10. 某校为改善校园环境,加大对绿化的投入,2021年对绿化投入资金10万元,2023年对绿化投入资金万元.现假定每年投入绿化资金的增长率相同,则该校投入绿化资金的年平均增长率为 .11. 某件商品的销售利润y(元)与商品单价x(元)之间满足 , 不考虑其他因素,该商品的单价定为元时,销售一件该商品获得的利润最大,最大利润为元.12. 如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米.水面下降1米时,水面的宽度为米.
 13. 如图是一座截面为抛物线的拱形桥,当拱顶离水面3米高时,水面宽l为6米,则当水面下降3米时,水面宽度为米.(结果保留根号)
13. 如图是一座截面为抛物线的拱形桥,当拱顶离水面3米高时,水面宽l为6米,则当水面下降3米时,水面宽度为米.(结果保留根号)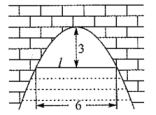
三、解答题
-
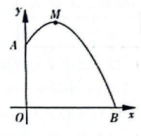
14. 如图,某幢建筑物从2.25米高的窗口A用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点M离墙1米,离地面3米,则水流下落点B离墙的距离是多少米?
 15. 某景区有两个景点需购票游览,售票处出示的三种购票方式如下:
15. 某景区有两个景点需购票游览,售票处出示的三种购票方式如下:方式1:只购买景点A,30元/人;
方式2:只购买景点B,50元/人﹔
方式3:景点A和B联票,70元/人.
预测,四月份选择这三种购票方式的人数分别有2万、1万和1万.为增加收入,对门票价格进行调整,发现当方式1和2的门票价格不变时,方式3的联票价格每下降1元,将有原计划只购买A门票的400人和原计划只购买B门票的600人改为购买联票.
(1)、若联票价格下降5元,则购买方式1门票的人数有万人,购买方式2门票的人数有万人,购买方式3门票的人数有万人.请计算门票总收入有多少万元?(2)、当联票价格下降x(元)时,请求出四月份的门票总收入w(万元)关于x(元)之间的函数表达式,并求出联票价格为多少元时,四月份的门票总收入最大?最大值是多少?四、综合题
-
16. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.
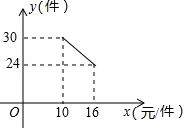 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?17. 掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为 , 当水平距离为3m时,实心球行进至最高点3m处.
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?17. 掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图1是一名女生投掷实心球,实心求行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图2所示,抛出时起点处高度为 , 当水平距离为3m时,实心球行进至最高点3m处.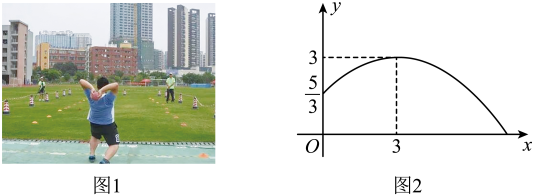 (1)、求y关于x的函数表达式;(2)、根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
(1)、求y关于x的函数表达式;(2)、根据兰州市高中阶段学校招生体有考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.