2023-2024学年冀教版初中数学九年级下册 30.2 二次函数的图像与性质同步分层训练基础题
试卷更新日期:2024-01-27 类型:同步测试
一、选择题
-
1. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度后,得到抛物线的解析式为( )A、 B、 C、 D、2. 已知抛物线 ( )过 , 两点,则下列关系式一定正确的是( )A、 B、 C、 D、3. 抛物线可由抛物线经过怎样的平移得到( )A、向上平移1个单位 B、向下平移1个单位 C、向左平移1个单位 D、向右平移1个单位4. 若一次函数y=(n+1)x+n的图象过第一、三、四象限,则函数y=nx2﹣nx( )A、有最大值 B、有最大值 C、有最小值 D、有最小值5. 在同一平面直角坐标系内,将函数y=2x2+4x﹣3的图象向右平移2个单位,再向下平移1个单位得到图象的顶点坐标是( )A、(﹣3,﹣6) B、(1,﹣4) C、(1,﹣6) D、(﹣3,﹣4)6. 已知点A(a,b),B(4,c)在直线y=kx+3(k为常数,k≠0)上,若ab的最大值为9,则c的值为( )A、 B、2 C、 D、17. 在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、
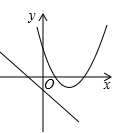 B、
B、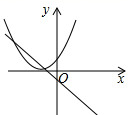 C、
C、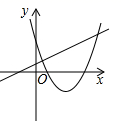 D、
D、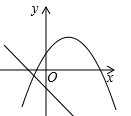 8. 把抛物线y=(x﹣1)2+2沿x轴向右平移2个单位后,再沿y轴向下平移3个单位,得到的抛物线解析式为( )A、y=(x﹣3)2+1 B、y=(x+1)2﹣1 C、y=(x﹣3)2﹣1 D、y=(x+1)2﹣2
8. 把抛物线y=(x﹣1)2+2沿x轴向右平移2个单位后,再沿y轴向下平移3个单位,得到的抛物线解析式为( )A、y=(x﹣3)2+1 B、y=(x+1)2﹣1 C、y=(x﹣3)2﹣1 D、y=(x+1)2﹣2二、填空题
-
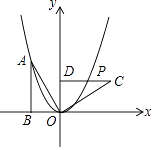
9. 二次函数的最小值为 .10. 抛物线的函数表达式为 , 若将轴向下平移1个单位长度,将轴向左平移2个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为.11. 若二次函数的图象开口向下,则的取值范围是 .12. 已知y=2x﹣1,且0≤x≤ , 若S=xy , 则S的最小值为 .13. 如图,Rt△OAB的顶点A(﹣4,8)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为
三、解答题
-
14. 在平面直角坐标系xOy中,有抛物线.(1)、若点在抛物线上,
①求抛物线的对称轴;
②若点也在抛物线上,求的取值范围;
(2)、当时,有已知点 , 若抛物线与线段AB只有一个公共点,结合函数图象,求的取值范围.15. 如图,某单位拟在一块空地上修建矩形植物园ABCD,其中一边靠墙,可利用的墙长不超过16米,另外三边由36米长的栅栏围成,设矩形ABCD中,垂直于墙的边米,面积为y平方米. (1)、y与x之间的函数关系式为 , 自变量x的取值范围为;(2)、若矩形ABCD的面积为154平方米,求x的值;(3)、当矩形ABCD的面积最大时,利用的墙长是多少米?并求此时的最大面积.
(1)、y与x之间的函数关系式为 , 自变量x的取值范围为;(2)、若矩形ABCD的面积为154平方米,求x的值;(3)、当矩形ABCD的面积最大时,利用的墙长是多少米?并求此时的最大面积.四、综合题
-
16. 如图,在矩形ABCD中,AB=2,BC=4,E,F,G,H四点依次是边AB,BC,CD,DA上一点(不与各顶点重合),且AE=AH=CG=CF,记四边形EFGH面积为S(图中阴影),AE=x.
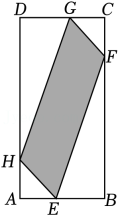 (1)、求S关于x的函数表达式,并直接写出自变量的取值范围.(2)、求x为何值时,S的值最大,并写出S的最大值.17. 如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形 . 设的长为 , 四边形的面积为 .
(1)、求S关于x的函数表达式,并直接写出自变量的取值范围.(2)、求x为何值时,S的值最大,并写出S的最大值.17. 如图,正方形纸片的边长为4,将它剪去4个全等的直角三角形,得到四边形 . 设的长为 , 四边形的面积为 .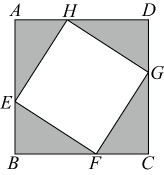 (1)、求关于的函数表达式;(2)、当取何值时,四边形的面积为10?(3)、四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(1)、求关于的函数表达式;(2)、当取何值时,四边形的面积为10?(3)、四边形的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.